Расчет полиспаст: схема полиспаста, назначение, устройство, виды

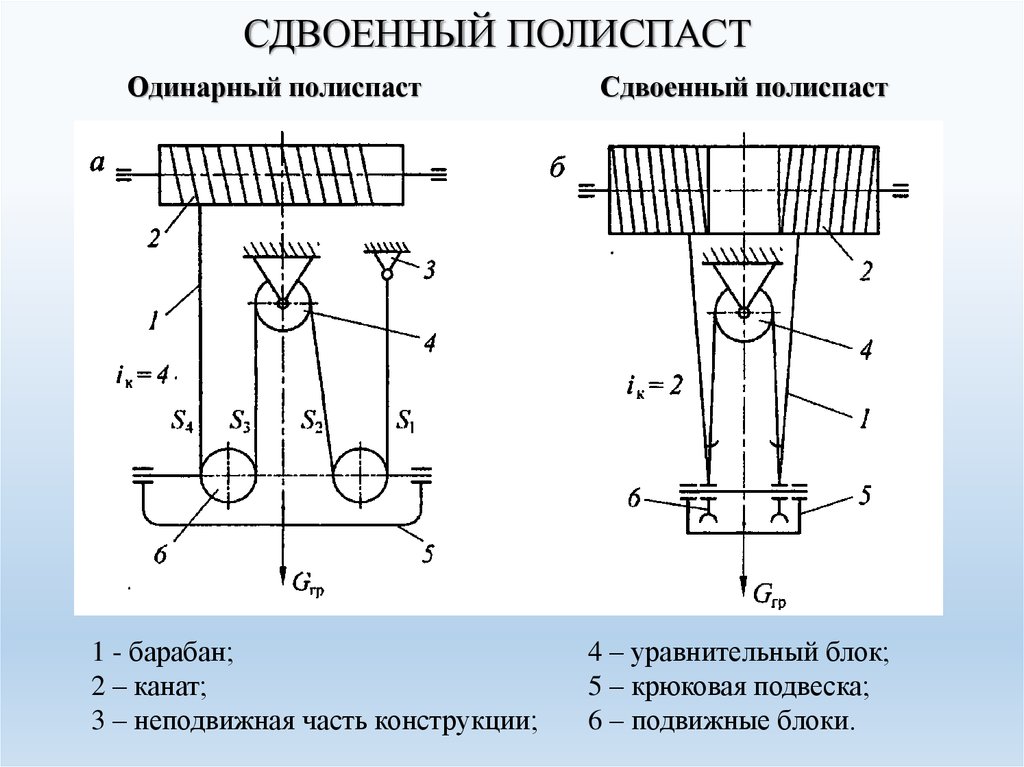
1. Расчет полиспаста

Схема полиспаста (рис 1).

1.1 Усилие в канате, набегающем на барабан

,

где m – кратность полиспаста, m=6 [1, табл. 2,2];

— КПД блока, принимаем=0,97 [1, табл. 2,1].

1.2 Расчетное разрывное усилие в канате

,

где k коэффициент запаса прочности, k=5.5 [1, табл. 2,3].

Выбираем канат [1, табл. III 1,1] двойной свивки типа ЛК-Р конструкции по ГОСТ 2688-80, диаметром d=19,5мм, маркированная группа 1764МПа,

2. Расчет стропов

2.1. Усилие в стропе

,

где — коэффициент неравномерности нагрузки ветви стропа,=1,4 [2, стр. 9];

m — число ветвей стропа, m=4;

— угол наклона ветвей стропа,принимаем.

2.

2 Разрывное усилие в стропе

,

где R_c – коэффициент запаса прочности стропа, R_c=6 [2, табл. 2,1].

Выбираем канат [1, табл. III 1,1] двойной свивки типа ЛК-Р конструкции по ГОСТ 2688-80, диаметром d=32мм, маркированная группа 1764МПа,

2.3 Высота строповки

,

принимаем

,

с учетом этого высота груза:

3. Расчет барабана

,

где e – коэффициент, зависящий от условий работы, принимаем е=20.

Принимаем d_бл=400мм; D_б=400мм.

Минимальная высота полиспаста

,

следовательно, длина каната, навиваемого на барабан

,

длина каната в одном витке на барабане

,

,

длина барабана при трехслойной навивке

,

проверка

4. Расчет мачты

Высота закрепления полиспаста

,

где h_A – расстояние от нижней части груза до места крепления полиспаста;

k_B – коэффициент запаса высоты.

,

,

длина консоли

,

,

,

.

5. Пространственное положение узлов

Точка 1: .

Точка 2: ,

.

Точка 3: ,

.

Точка 4: ,

.

Точка 5: ,

,

.

Для сечения 1:

,

,

.

Разрывное усилие в канате растяжки

,

Выбираем канат [1, табл. III 1,1] двойной свивки типа ЛК-Р конструкции 6х19(6+6+6/6)+1_о.с. по ГОСТ 2688-80, диаметром d=19,5мм. Маркировочная группа 1764МПа, Р_разр.=209000 Н

6. Выбор электродвигателя

,

выбираем электродвигатель MTF 412-6 [1, табл. III 3,5], имеющий при ПВ=25% номинальную мощность N=40кВт; b

31=198мм, частота вращения n_дв=960мин^-1, вес двигателя G_дв=210кг.

7. Выбор редуктора

Частота вращения барабана

,

необходимое передаточное число редуктора

,

требуемое межосевое расстояние

,

выбираем редуктор [1, табл. III 4,2] типа Ц2-500: передаточное число u=24,9, мощность N=52,7кВт, n=750мин^-1.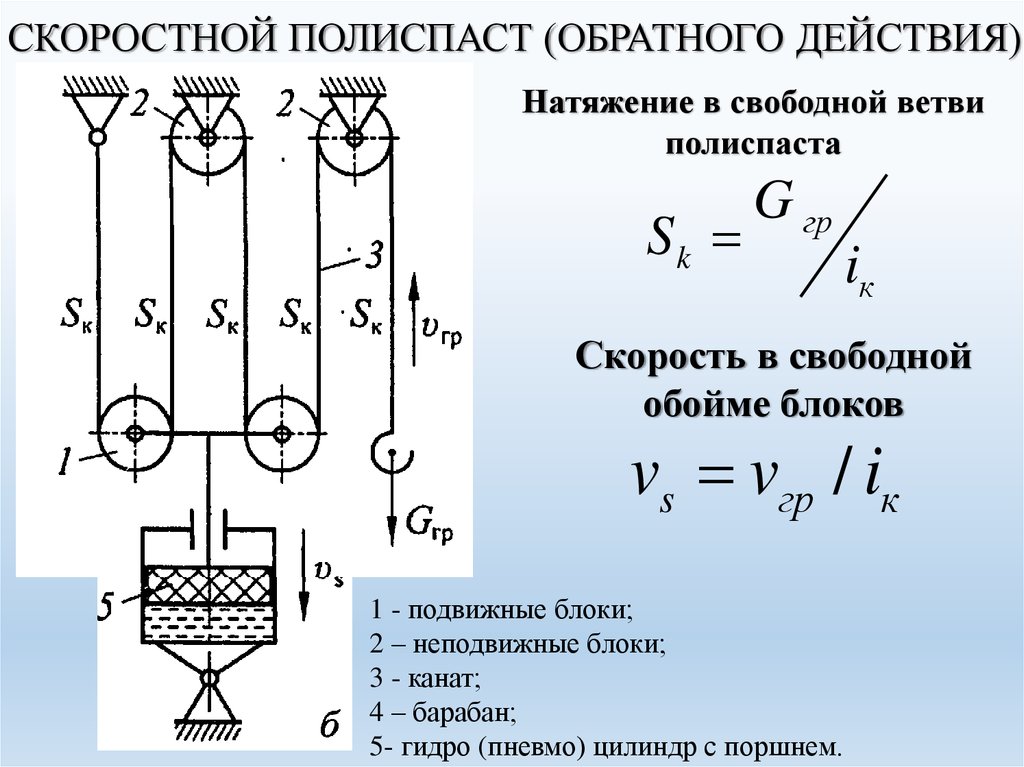

8. Значение реакций опор

,

усилие, действующее в стержне

.

9. Подбор поперечного сечения мачты

Определим необходимую площадь сечения мачты

,

выбираем трубу диаметром D=325мм, толщина стенки 40мм, площадь поперечного сечения,

моменты инерции сечения

, моменты сопротивления сечения

,

максимальный момент в мачте

,

Проверяем мачту по условию прочности

,

.

Условие выполняется.

10. Расчет противовеса лебедки

Из условия устойчивости:

,

где М_вост, М_опр – соответственно восстанавливающий о опрокидывающий моменты.

С учетом этого вес противовеса

,

где G_л – вес лебедки,

l, l₁, l₂ – размеры лебедки.

,

,

,

из конструктивных соображений ,

с учетом этого

Определяем высоту противовеса

,

где a_пр, b_пр – размеры противовеса (принимаем конструктивно).

11. Расчет узла крепления полиспаста

Условие прочности:

,

где A — площадь поперечного сечения болта;

— допускаемое напряжение растяжения. Определим диаметр болта

принимаем болт М36.

Произведем расчет с помощью программного комплекса «ЛИРА» 9.0 D. Результаты расчетов представим в виде пояснительной записки.

П О Я С Н И Т Е Л Ь Н А Я З А П И С К А

Имя задачи: Фик

Расчет плоской системы, состоящей из стержневых элементов на статические нагрузки

Объект: Монтажная мачта Q = 19т.

Организация: ЗГИА, каф. МОМЗ

Выполнил: студент гр. ММО -99 д Фик В. А.

Проверил: доцент Малышев Г. П.

Запорожье

2003г.

ВВЕДЕНИЕ

Расчет выполнен программным комплексом «ЛИРА».

В основу расчета положен метод конечных элементов в перемещениях. В качестве основных неизвестных приняты следующие перемещения узлов:

X линейное по оси X

Z линейное по оси Z

UY угловое вокруг оси Y

В ПК «ЛИРА» реализованы положения следующих разделов

СНиП (с учетом изменений на 1.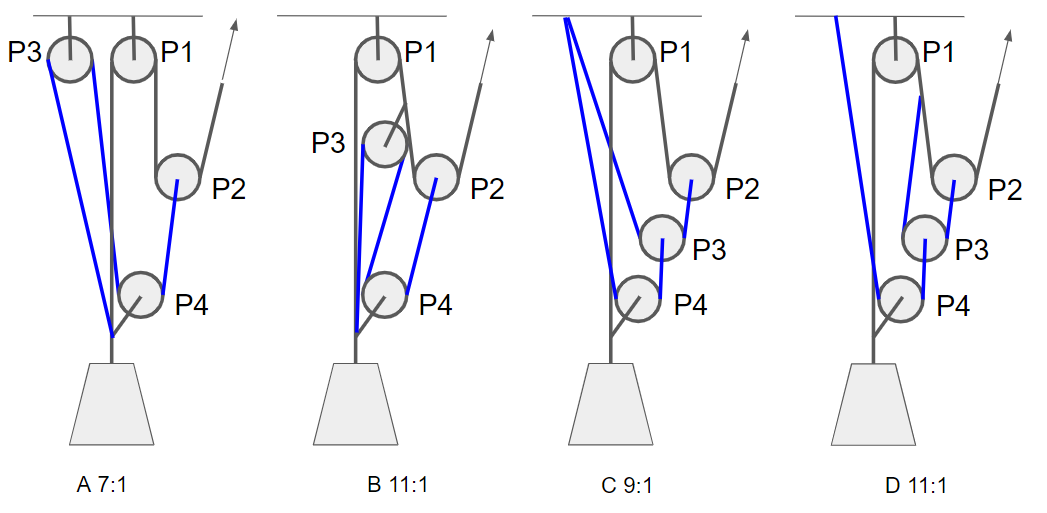 01.97):

СНиП 2.01.07-85* нагрузки и воздействия

СНиП 2.03.01-84* бетонные и железобетонные конструкции

СНиП II-7-81* строительство в сейсмических районах

СНиП II-23-81* стальные конструкции

Типы используемых конечных элементов указаны в документе 1. В этом документе, кроме номеров узлов, относящихся к соответствующему элементу, указываются также номера типов жесткостей.

В расчетную схему включены следующие типы элементов:

Tип 10. Универсальный пространственный стержневой КЭ.

Координаты узлов и нагрузки, приведенные в развернутых документах 4,6,7, описаны в правой декартовой системе координат.

Расчет выполнен на следующие загружения:

Загружение 1 — статическое загружение

ЧТЕНИЕ РЕЗУЛЬТАТОВ СЧЕТА

Результаты счета разбиты на следующие разделы:

статья про полиспасты, часть 3

Как посчитать реальный выигрыш в силе от полиспаста?

Остальные части статьи: первая, вторая и четвёртая

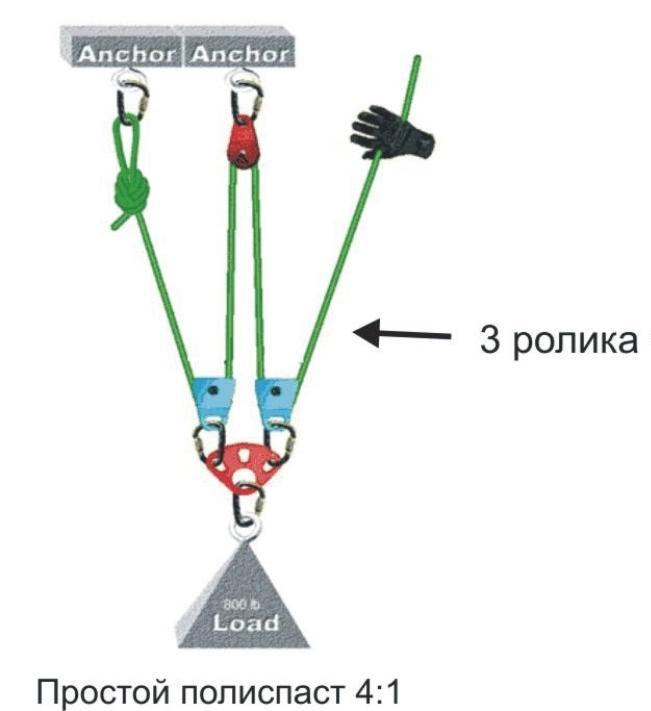
Расчёт реального выигрыша в силе

   Для того, чтобы рассчитать реальный выигрыш вашего полиспаста, необходимо знать эффективность используемых блоков (их КПД), выражаемую числом от 0 до 1 (или от 0% до 100%, если считать в процентах).

Если верёвка очень большого диаметра или слишком жёсткая, то эффективность блоков в составе полиспаста будет ниже заявленной производителем и это необходимо учесть, скорректировав КПД блоков.

Для расчёта реального выигрыша простого полиспаста надо рассчитать нагрузку на каждой рабочей ветви верёвки полиспаста и сложить их. Для расчёта выигрыша сложного полиспаста необходимо рассчитать и перемножить реальные выигрыши составляющих его простых полиспастов.

В таблице ниже приведены примерные реальные выигрыши наиболее распространённых полиспастов с использованием различных видов блоков. В каждом случае предполагается, что в полиспасте использовались блоки с одинаковой эффективностью.

Приведена примерная эффективность блоков (роликов).

ТВ — теоретический выигрыш (выигрыш в силе идеального полиспаста без трения).

Из данной таблицы можно сделать следующие выводы:

• сложные полиспасты эффективнее простых с точки зрения выигрыша в силе (но при этом менее эффективны по числу перестановок полиспастов).
• каждый следующий добавляемый блок увеличивает выигрыш меньше, чем предыдущий, то есть, например, при сборе полиспаста из карабинов наращивать кратность полиспаста после х4 не имеет смысла.

Блоки с различной эффективностью

   В первой части нашей статьи было сделано утверждение, что блоки должны располагаться по увеличению эффективности от груза к тянущему (то есть, наиболее эффективный блок должен быть ближе всех к тянущему).

Проиллюстрируем и докажем это утверждение. Соберём простой полиспаст с теоретическим выигрышем в силе в 4 раза. В качестве блоков используем карабин, ролик с низкой эффективностью и ролик с высокой эффективностью.

Рассмотрим 3 варианта взаимного расположения блоков, в порядке от тянущего:

1. Карабин, блок с низкой эффективностью, блок с высокой эффективностью.
2. Блок с высокой эффективностью, карабин, блок с низкой эффективностью.
3. Блок с высокой эффективностью, блок с низкой эффективностью, карабин.

   После расчётов с принятым КПД блоков получаем следующие результаты:

1. Выигрыш в 2.165 раза.

2. Выигрыш в 2.665 раза.

3. Выигрыш в 2.845 раза.

Следовательно, наиболее эффективным является полиспаст, в котором блоки расположены по убыванию эффективности от тянущего.

Расчёт реального выигрыша простого полиспаста в силе, с использованием формул

   Расчитать реальный выигрыш можно не расписывая каждую ветвь, просто используя формулы.

   Случай 1 — все блоки имеют одинаковый КПД (К) и используется m блоков, m — целое число от 1 до бесконечности.

   Тогда реальный выигрыш РВ рассчитывается по следующей формуле (справа).

   Пример.

   У нас 3 блока с КПД 0.8. Значит, у нас K=0.8, m=3.

   Из трёх блоков мы можем собрать простой чётный полиспаст с теоретическим выигрышем в силе в 4 раза.

   Рассчитаем его реальный выигрыш:

Таким образом, реальный выигрыш получился 2.952

Случай 2 — также используем m блоков, но все блоки имеют различный КПД. Первый блок имеет КПД К1, второй К2 и так далее до блокаm с КПД Кm. Нумерация блоков от тянущего.

Тогда реальный выигрыш РВ рассчитывается по следующей формуле:

Пример.

   Применим формулу к рассмотренному выше случаю, в котором иллюстрировалась последовательность расположения блоков с разным КПД. То есть у нас есть 3 блока, первый имеет КПД 0.9, второй — 0.7, третий — 0.5. Таким образом, m=3, K1=0.9, K2=0.7, K3=0.5.

   Рассчитаем его реальный выигрыш.

PB = 1+K1+K1*K2+K1*K2*K3 = 1+0.9+0.9*0.7+0.5*0.9*0.7 = 1+0.9+0.63+0.315 = 2.845

   Таким образом, реальный выигрыш получился 2.845, что согласуется с результатом расчёта другим способом.

   Для случая, когда все блоки имеют одинаковый КПД (К) можно легко получить априорную оценку количества эффективных блоков. Здесь под количеством эффективных блоков понимаем такое количество блоков, при котором добавление ещё одного блока не приведёт к желаемому увеличению реального выигрыша в силе.

   Желаемое увеличение выигрыша в силе — некоторая величина, увеличение выигрыша на которую вы считаете не имеющим смысла. Назовём эту величину Delta. Т.е. пусть у вас есть полиспаст с выигрышем 4.5. Добавление ещё одного блока увеличит выигрыш на Delta=0.1, т.е. выигрыш станет 4.6. Очевидно, что такое изменение выигрыша в силе бесполезно, и при этом увеличится расход верёвки.

   Таким образом, мы можем теперь рассчитать количество эффективных блоков КБ по формуле:

где ln — натуральный логарифм, квадратные скобки — операция взятия целой части.

Ну а теперь можно приступать к сборке полиспаста =).

Пример.

   У нас есть ролики Petzl Fixe, с КПД 0.7. Увеличение выигрыша менее, чем в 0.2 раза для нас не имеет смысла. То есть K=0.7, Delta=0.2 Теперь рассчитаем количество блоков КБ:

   Получаем, что нам надо задействовать 4 блока, а дальнейшее добавление блоков не будет давать достаточного для нас увеличения выигрыша.

   Также для случая блоков с одинаковым КПД можно рассчитать предельно возможный для данного типа блоков (с данным КПД) теоретический выигрыш maxPB — т.е. такой выигрыш, увеличения которого невозможно добиться, сколько блоков не добавляли бы в полиспаст.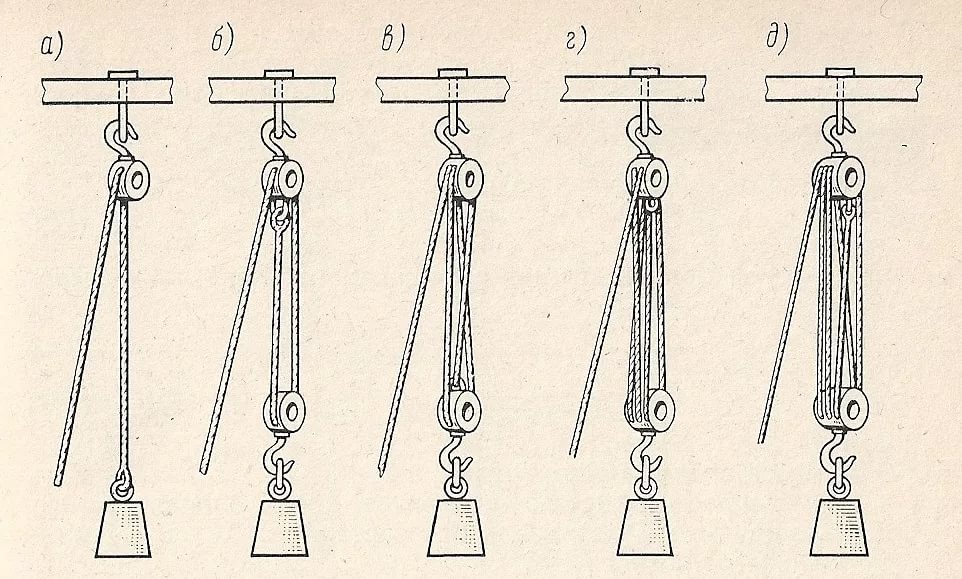

maxPB=1/(1-K)

   Примеры.

   Для роликов Petzl Fixe, с КПД 0.7 предельный реальный выигрыш: maxPB=1/(1-0.7)=3.(3)

   Для карабинов с КПД 0.5 предельный реальный выигрыш: maxPB=1/(1-0.5)=2

ЧАСТЬ ПЕРВАЯ >>

Простые и сложные полиспасты. Расчёт кратности полиспаста.

ЧАСТЬ ВТОРАЯ >>

Прикрепление полиспаста к веревке и безопасность работ

ЧАСТЬ ЧЕТВЁРТАЯ >>

Комплексные полиспасты и прочие элементы высшего пилотажа

ИСПАНСКИЙ ПОЛИСПАСТ >>

Полиспаст без блоков и карабинов, фиксирующийся самостоятельно

При создании статьи были использованы материалы команды WS RopeJump, статьи Industrial Quality and Safety Association, информация с официального сайта компании Petzl , работа «Полиспасты для спасательных работ» Фёдора Фарберова и личный опыт авторов.

Настоящий материал не претендует на звание истины в последней инстанции а лишь преследует цель познакомить читателей с практическими способами подъёма и перемещения грузов с помощью полиспастных систем.

Как рассчитать системы шкивов

••• Aon_skynotlimit/iStock/GettyImages

Обновлено 29 апреля 2018 г.

Автор Angel Coswell

Вы можете рассчитать силу и действие систем шкивов, применяя законы движения Ньютона. Второй закон работает с силой и ускорением; третий закон указывает направление сил и то, как сила натяжения уравновешивает силу тяжести.

Блоки: подъемы и опускания

Блок представляет собой установленное вращающееся колесо с изогнутым выпуклым ободом с канатом, ремнем или цепью, которые могут перемещаться по ободу колеса для изменения направления тягового усилия. Он изменяет или уменьшает усилие, необходимое для перемещения тяжелых объектов, таких как автомобильные двигатели и лифты. Базовая система шкивов имеет объект, соединенный с одним концом, в то время как контролирующая сила, например, от мышц человека или двигателя, тянет с другого конца. В системе шкивов Atwood оба конца каната шкива соединены с объектами. Если два объекта имеют одинаковый вес, шкив не будет двигаться; однако небольшой рывок с любой стороны будет перемещать их в одну или другую сторону. Если грузы разные, то более тяжелый груз будет ускоряться вниз, а более легкий – вверх.

Базовая система шкивов

Второй закон Ньютона F (сила) = M (масса) x A (ускорение) предполагает, что шкив не имеет трения, и вы игнорируете массу шкива. Третий закон Ньютона гласит, что на каждое действие есть равное и противоположное противодействие, поэтому общая сила системы F будет равна силе веревки или T (натяжение) + G (сила тяжести), тянущей груз. В базовой системе шкивов, если вы приложите силу, превышающую массу, ваша масса ускорится, в результате чего F станет отрицательным. Если масса движется вниз с ускорением, F положительна.

Рассчитайте натяжение веревки, используя следующее уравнение: T = M x A. Четыре примера, если вы пытаетесь найти T в базовой системе шкивов с присоединенной массой 9 г, ускоряющейся вверх со скоростью 2 м/с², тогда T = 9 г. x 2 м/с² = 18 г/с² или 18 Н (ньютонов).

Рассчитайте силу тяжести, воздействующую на базовую систему шкивов, используя следующее уравнение: G = M x n (ускорение свободного падения). Гравитационное ускорение является постоянной величиной, равной 9,8 м/с². Масса M = 9 г, поэтому G = 9 г x 9.0,8 м/с² = 88,2 г/с² или 88,2 ньютона.

Вставьте только что вычисленные вами натяжение и гравитационную силу в исходное уравнение: -F = T + G = 18 Н + 88,2 Н = 106,2 Н. Сила отрицательна, потому что объект в системе шкивов ускоряется вверх. Отрицательное значение силы переходит в раствор, так что F = -106,2 Н.

Система шкивов Atwood

Уравнения F(1) = T(1) — G(1) и F(2) = -T(2)+ G(2) предполагают, что шкив не имеет трения или массы. Также предполагается, что масса два больше массы один. В противном случае поменяйте уравнения местами.

Рассчитайте натяжение с обеих сторон системы шкивов с помощью калькулятора, чтобы решить следующие уравнения: T(1) = M(1) x A(1) и T(2) = M(2) x A(2) . Например, масса первого объекта равна 3 г, масса второго объекта равна 6 г, а обе стороны веревки имеют одинаковое ускорение, равное 6,6 м/с². В этом случае T(1) = 3g x 6,6 м/с² = 19,8 Н и T(2) = 6 г x 6,6 м/с² = 39,6 Н.

Рассчитайте силу тяжести, действующую на базовую систему шкивов, используя следующее уравнение: G(1) = M(1) x n и G(2) = M(2) x n. Ускорение свободного падения n является константой, равной 90,8 м/с². Если первая масса M(1) = 3 г, а вторая масса M(2) = 6 г, то G(1) = 3 г x 9,8 м/с² = 29,4 Н и G(2) = 6 г x 9,8 м/с² = 58,8. Н.

Вставьте напряжения и гравитационные силы, рассчитанные ранее для обоих объектов, в исходные уравнения. Для первого объекта F(1) = T(1) — G(1) = 19,8N — 29,4N = -9,6N, а для второго объекта F(2) = -T(2) + G(2) = -39,6 Н + 58,8 Н = 19,2 Н. Тот факт, что сила второго объекта больше силы первого объекта и что сила первого объекта отрицательна, показывает, что первый объект ускоряется вверх, а второй объект движется вниз.

Вещи, которые вам понадобятся

• Калькулятор
• Вес объекта или объектов, используемых в системе шкивов

Связанные статьи

Ссылки

• законы, Шкив, стр. 155
• Соединения: Шкив
• Университет Джорджа Вашингтона: Шкивы

Об авторе

Энджел Косуэлл начала свою писательскую карьеру в 2008 году. и финансирование. В 2008 году она получила степень магистра физики со специализацией в области инженерии в Университете штата Юта.

Rope Rescue Расчет МА путем подсчета строп

Rope Rescue Расчет МА по подсчету строп

Этот веб-сайт требует javascript для правильной работы. Узнайте, как включить JavaScript.

На предыдущей странице объяснялось, как для расчета механического преимущества канатно-шкивной системы с использованием Т-системы. На этой странице объясняется метод «подсчета строк». «Считать строки» легко использовать метод, который лучше всего работает с простыми системы механических преимуществ, хотя этот метод можно использовать с составные системы.

Простые системы

Чтобы рассчитать механическое преимущество путем подсчета линий, подсчитайте количество сегментов каната (так называемых «линий»), которые либо связаны с грузом, либо соединенный со шкивом, который будет двигаться с той же скоростью, что и груз.

Ссылаясь на следующую иллюстрацию, три «линии» соответствуют этому критерию, поэтому это система 3:1.

Составные системы

Расчет механического преимущества составных систем такелажа с использованием «подсчета Метод линий» немного сложен. Как вы, возможно, помните, метод составная система определяется как одна простая система тянет за собой другую простую систему. Для расчета механич. Чтобы воспользоваться этими системами, используя метод «подсчета строк», вам необходимо:

1. Изолируйте простые системы внутри составной системы.
2. Используйте метод «подсчет линий», чтобы определить механическое преимущество отдельные простые системы.
3. Умножьте механическое преимущество отдельных систем для определения Общее механическое преимущество.

Тест на преимущество в механике

Проверьте, можете ли вы использовать метод «подсчета строк» ​​для решения следующих систем. (Нажмите на иллюстрации, чтобы увеличить их.