60. Сжимаемость грунтов. Деформативные характеристики грунтов. Испытания грунта методом одноосного сжатия. Закон компрессии.
Наиболее важным деформационным свойством грунтов является их сжимаемость. Сжимаемостью грунтов называется их способность уменьшаться в объеме под действием внешней нагрузки. Сжимаемость зависит от пористости грунтов, гранулометрического и минералогического состава, природы внутренних структурных связей и характера нагрузки.
Деформативными характеристиками сжимаемости являются: коэффициент сжимаемости m0, МПа-1; коэффициент относительной сжимаемости mV, МПа -1; модуль общей деформации Ео, МПа и структурная прочность грунта Рстр, МПа. Одним из способов определения характеристик сжимаемости в лабораторных условиях являются компрессионные испытания. Это испытания грунта в условиях одноосного сжатия без возможности бокового расширения. Компрессионное сжатие моделирует процесс уплотнения грунта под центром фундамента. Компрессионные испытания грунтов производят в одометрах – приборах с жесткими металлическими стенками, препятствующими боковому расширению грунта при сжатии его вертикальной нагрузкой. При испытаниях происходит уплотнение грунта за счет уменьшения объема пор и влажности.
Рис. Схема испытания образца грунта на сжатие в одометре.
При испытании прикладываем на образец грунта нагрузку Р1 – произойдет уплотнение грунта, и коэффициент пористости станет е1.
Затем прикладываем нагрузку Р2, получим е2 и т.д. (4–5 ступеней).
После заданного нагружения будем снимать нагрузку и наблюдать за результатами. По результатам испытаний строим график компрессионной кривой (к.к).
Графическое представление компессионных испытаний в одометре с построением прямой и обратной ветвей компрессионных кривых (к.к.).
Компрессия- это сжатие грунта без возможного бокового расширения.
Закон уплотнения (Закон компрессии)
изменение коэффициента пористости грунта прямо пропорционально изменению давления.
Правая часть этого равенства является относительной деформацией грунта. Поскольку для определенного грунта и данного изменения давления величинапостоянна, относительная деформация грунта прямо пропорциональна давлению. Следовательно, грунт можно считать линейно деформируемым телом.-
Однако в ряде случаев это положение приводит к значительным расхождениям между рассчитанными и наблюдаемыми в натуре деформациями.
Из графика компрессионной кривой видно, что происходит необратимое уплотнение грунта. Обратная ветвь к.к. – возможность поднятия дна котлована, имеет значение при глубоких котлованах(гидротехническое строительство).
На небольшом участке рассмотрим приращение нагрузки ∆Р и получим соответственно ∆е. Заменим дугу прямой и рассмотрим угол α.
В этой формуле знак (–) означает, что с увеличением нагрузки α – уменьшается. В дифференциальной форме:
dе = –tgαdР
tgα = mо и тогда de = –mоdP – основная математическая форма закона компрессии.
Относительное изменение коэффициента пористости пропорционально изменению нагрузки (для малых интервалов нагрузок).
Компрессионная кривая позволяет судить о сжимаемости грунта.
α – может характеризовать сжимаемость.
Пример изменения угла наклона к.к. для мало и сильно сжимаемого грунтов.
Возьмем произвольную точку i на прямой, в пределах отрезка Р1 – Р2. Составим уравнение для этой точки, исходя из начального параметра е0.
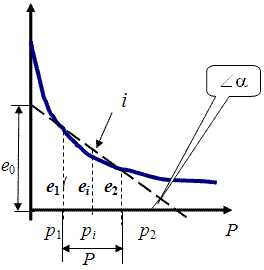
еi = е0
– рi tgα – это основное уравнение, характеризующее компрессию в выбранном варианте.Рассмотрим подробнее .
где m<o – коэффициент сжимаемости грунта.
Для того чтобы получить mo, необходимо выделить определенный интервал давлений.
Р1 – напряжение от собственного веса грунта
Р – дополнительное давление от внешней нагрузки
Р2 – полное напряжение (Р2 = Р1 + Р)
Окончательно:
В соответствии с полученными значениями коэффициента относительной сжимаемости СП (СНиП) определяет 3 категории грунта:
mo < 0,005 – грунт мало сжимаемый.
mo = 0,005÷0,05 – грунт средне сжимаемый.
mo > 0,05 – грунт сильно сжимаемый.
При изысканиях отбирают пробы грунта, строят график к.к. и определяют m
Основной расчет оснований по II предельному состоянию – по деформациям. В формулу расчета осадки S=hmvP входит величина коэффициента относительного сжатия грунта .
Таким образом, mо является той характеристикой, которая, как правило, решает выбор основания: можно строить или нельзя (тогда возникает необходимость перехода на искусственное основание).
существует еще одна характеристика сжатия грунта: Е0 – модуль общей деформации грунта.
Е0 – характеризует упругие + остаточные деформации
(Эти деформации не разделяются, так как в большинстве случаев для здания это не имеет никакого значения.)
Модуль общей деформации может быть определен следующим выражением:
μ – коэффициент Пуассона (бокового расширения грунта).studfiles.net
Сжимаемость грунтов. Закон уплотнения
Сжимаемость грунтовявляется характернейшим их свойством, существенно отличающим грунты от массивных горных пород и других твердых тел, и заключается в способности грунтов изменять (иногда значительно) свое строение (упаковку твердых частиц) под влиянием внешних воздействий (сжимающей нагрузки, высыхания, коагуляции коллоидов и пр.) на более компактное за счет уменьшения пористости грунта.
Уменьшение пористости грунтов при более компактной упаковке частиц происходит как вследствие возникновения некоторых местных сдвигов частиц и соскальзывания более мелких частиц в поры грунта, так (особенно у дисперсных водонасыщенных глинистых грунтов) и вследствие изменения толщины водно-коллоидных оболочек минеральных частиц под влиянием увеличения давления, высыхания, коагуляции и пр.
Кроме того, на переупаковку частиц влияет ползучесть скелета грунта и оболочек прочносвязанной воды (которые также можно относить к скелету грунта), обусловленная искажением формы кристаллических решеток минеральных частиц и медленным вязким течением молекулярных слоев прочносвязанной воды.
Следует здесь же отметить, что для грунтов полностью водонасыщенных изменение пористости возможно лишь при изменении их влажности (выдавливании или всасывании воды) и некоторого внутри-объемного сжатия газовых включений; для грунтов же неводонасыщенных оно может происходить и при сохранении их влажности.
Изменение объема пор дисперсных грунтов при высыхании (в процессе обезвоживания диффузных оболочек и увеличения капиллярного сжатия), а также в результате медленных физико-химических процессов (например, старения коллоидов) учитывают лишь в отдельных исключительных случаях, и основным процессом изменения объема грунтов будет уплотнение
их под нагрузкой.Следует различать уплотняемость грунтов при кратковременном действии динамических нагрузок (механическую) и уплотнение при длительном действии постоянной статической нагрузки (компрессию, консолидацию и пр.).
При механическом воздействии вибрационными, трамбующими и подобными механизмами хорошо уплотняются лишь маловлажные рыхлые песчаные и неводонасыщенные грунты, имеющие жесткие контакты между минеральными частицами, которые при этих воздействиях легко нарушаются, что и обусловливает перегруппировку частиц и более плотную их упаковку. В водонасыщенных же песках динамические нагрузки вызывают значительные напоры в воде, грунт взвешивается в некоторой области и при определенных условиях разжижается, растекаясь по большой площади. Однако чем больше внешнее давление на поверхность грунта, подвергаемого динамическому воздействию (например, вибрационному), тем менее оно эффективно, так как труднее преодолеваются усилия в точках контакта частиц.
В глинистых грунтах, которые вследствие их связности при динамических нагрузках уплотняются очень мало, возникающие в воде напоры при незначительной водопроницаемости этих грунтов погашаются на весьма малом расстоянии и разжижения не происходит.
При уплотнении грунтов сплошной постоянной нагрузкой (компрессии грунтов) следует рассматривать, по крайней мере, два диапазона давлений: 1 — когда внешнее давление меньше прочности структурных связей и 2 — когда эти связи преодолены.
В первом случае, как показывают исследования, проведенные в МИСИ и других исследовательских организациях, уплотнения грунтов не происходит, так как возникающие под действием внешней нагрузки деформации в этом случае будут упругими деформациями структурных связей и грунт будет деформироваться как сплошное квазитвердое тело.
Во втором случае, т. е. когда жесткие структурные связи преодолены (при давлениях, больших структурной прочности), грунты будут уплотняться значительно, причем для грунтов с водно-коллоидными связями уплотнение будет происходить за счет сжатия водно-коллоидных оболочек минеральных частиц с выдавливанием некоторого количества воды, а также в известной мере и за счет ползучести скелета грунта. Выдавливание же воды для данных глинистых грунтов возможно лишь при напоре, вызываемом действием внешней нагрузки, большем некоторой начальной величины.
Для грунтов, обладающих одновременно и мягкими водно-коллоидными и жесткими кристаллизационными связями, процесс уплотнения будет значительно сложнее.
Зависимость между влажностью, давлением и коэффициентом пористости. Для установления основных показателей сжимаемости грунта производят испытания его на уплотнение под нагрузкой в условиях одномерной задачи, когда деформации грунта могут развиваться только в одном направлении и никакие другие силы, кроме внешней нагрузки, не действуют.
При испытании водонасыщенного грунта его поверхность покрывают слоем воды, что позволяет избежать высыхания грунта в процессе опыта (который длится обычно от нескольких часов до нескольких дней), а следовательно, избежать развития в нем сил капиллярного давления.
Для испытания грунта на сжимаемость применяют приборы с жесткими стенками (одометры) для обеспечения сжатия грунта только в одном направлении (без возможности его бокового расширения – рис. 13, а).
Рис. 13. Схемы компрессионного сжатия грунта в жестком кольце (а) и при сплошной нагрузке (б)
Подобные граничные условия соответствуют в натуре сжатию отдельного слоя грунта под действием сплошной равномерно распределенной нагрузки (например, веса вышележащих слоев грунта — рис. 13, б). Нагрузку на поверхность грунта прикладывают отдельными возрастающими ступенями (например, 0,05; 0,10; 0,25; 0,5; 1,0; 2,0; 4,0 кгс/см2, соответственно 0,005; 0,010; 0,025; 0,05; 0,1; 0,2; 0,4 МПа), так как чем более будет уплотнен грунт предыдущей ступенью нагрузки, тем меньше будут его деформации и требуется большая точность измерений.
Опытами (проф. Терцаги и др.) было установлено, что для водонасыщенных, но маловодопроницаемых глинистых грунтов каждому приращению внешнего давления соответствует вполне определенное изменение влажности. Зависимость между влажностью и давлением можно изобразить в виде графика (рис. 14, а), который носит название компрессионной кривой. Так как для полностью водонасыщенных грунтов существует закономерная связь между влажностью и коэффициентом пористости [зависимость e = ωmaxγs], то компрессионную кривую (рис. 14, а) легко перестроить в координатах коэффициент пористости — давление (рис. 14, б).
Дальнейшие исследования показали, что компрессионные кривые применимы для оценки сжимаемости любых дисперсных материалов (связных, сыпучих), но для материалов водопроницаемых (например, песков) не могут быть построены по изменению влажности, так как при нагрузке этих материалов влажность восстанавливается почти мгновенно.
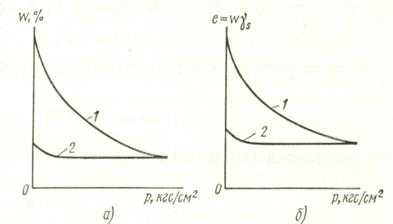
Рис. 14. Компрессионные кривые для глинистого грунта: 1 – кривые уплотнения; 2 – кривые разуплотнения (набухания)
Более общим методом построения компрессионных кривых является метод определения коэффициента пористости по осадкам образца грунта при уплотнении их в компрессионном приборе.
Если обозначить:
e0 — начальный коэффициент пористости грунта;
ei — коэффициент пористости грунта при любой ступени нагрузи;
si — полная осадка образца при данной нагрузке (рi,), измеренная от начала загружения;
Δni — изменение пористости грунта (объема пор) от начала загружения;
h — начальная высота образца грунта,
то, учитывая, что коэффициент пористости есть отношение объема пор к объему твердых частиц, будем иметь
ei = e0 – Δni/m. (15)
Так как для образца грунта, испытываемого без возможности бокового расширения, изменение объема пор Δni — численно равно произведению осадки si на площадь образца F, т. е.
Δni = siF, (16)
а объем твердых частиц во всем объеме грунта, учитывая выражение m = 1/(1 + e),
m = Fh · 1/(1 + e0) (17)
то, подставляя (в2) и (в3) в (в1), получим
ei = e0– (1 + e0)si/ h(1) (18)
Формулой (15) и пользуются для вычисления коэффициентов пористости, соответствующих данным ступеням нагрузки, а по ним строят и всю компрессионную кривую.
В ряде случаев (например, при оценке деформируемости просадочных грунтов и учете нелинейности сжатия при большом диапазоне давлений) в качестве характеристики сжимаемости грунтов применяется и так называемый модуль осадки (предложенный проф. Н. Н. Масловым, 1941) εp = si/h — относительная деформация грунта при данном давлении, выраженная в промиллях (мм/м).
Для грунтов естественной ненарушенной структуры компрессионная кривая имеет два участка (рис. 15): первый — до давлений, не превосходящих структурной прочности грунта рстр, с очертанием, близким к линейному, и очень малыми изменениями коэффициента пористости, и второй — криволинейный, со значительными изменениями коэффициента пористости, что указывает на уплотнение грунта под нагрузкой, превосходящей структурную прочность грунта. При меньших же нагрузках уплотнения грунта не происходит.
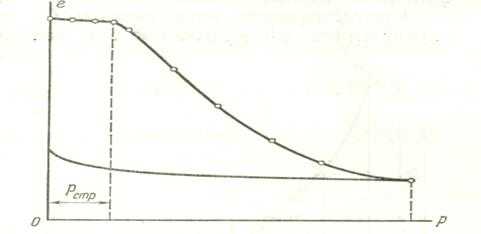
Рис. 15. Компрессионные кривые для образцов грунта ненарушенной структуры
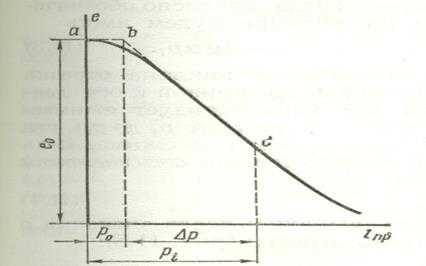
Рис. 16. Компрессионная кривая в полулогарифмических координатах
В дальнейшем мы будем рассматривать компрессионные кривые только при давлениях, больших структурной прочности грунтов.
Что касается величины структурной прочности грунтов рстр, то, как будет показано в последующих главах, она является весьма важной характеристикой грунтов. Величину ее можно определить по компрессионной кривой ненарушенной структуры, испытывая грунты (до достижения структурной прочности) весьма малыми ступенями нагрузки (примерно 0,02-0,10 кгс/см2, 0,002-0,010 МПа), тогда резкий перелом компрессионной кривой и будет соответствовать достижению структурной прочности сжатия грунта (рис. 15).
Другой метод определения структурной прочности предложен проф. Е. И. Медковым по результатам испытания бокового давления грунта при трехосной компрессии и соответствует давлению, при котором практически отсутствует боковое давление грунта.
Определение указанных выше давлений требует разработки специальной методики испытания, и в настоящее время величина структурной прочности может быть определена лишь с известным приближением, зависящим, главным образом, от точности измерений.
Если начертить компрессионную кривую в полулогарифмических координатах (рис. 16), то изменения коэффициента пористости грунта (для давлений, больших структурной прочности) будут линейно зависеть от логарифма изменений внешнего давления. Тогда уравнение компрессионной кривой для большого диапазона давлений может быть представлено в виде
ei = e0 – Сc ln (pi/p0), (19)
где е0и p0 — начальные коэффициент пористости и давление, близкое величине структурной прочности; eiи рi — коэффициент пористости и давление, соответствующее i-й ступени нагрузки; Сс — коэффициент компрессии.
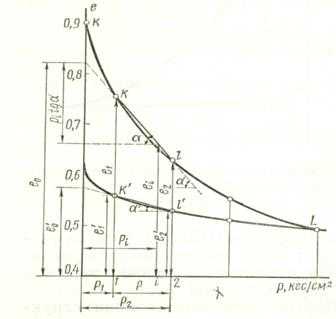
Рис. 17. Определение параметров отрезка компрессионной кривой
Коэффициент компрессии Сс есть тангенс угла наклона полулогарифмической кривой к оси давлений и численно равен разности коэффициента пористости при рi=е, т. е. при pi = 2,72 кгс/см2; (~0,272 МПа) и р0 = 1 кгс/см2, так как при
pi = е lnpi= 1.
Этот коэффициент (по размерности отвлеченное число) характеризует сжимаемость грунтов в большом диапазоне давлений.
Если ограничиться небольшим изменением давлений (порядка 1 — 3 кгс/см2, 0,1 — 0,3 МПа, что обычно и имеет место в основаниях сооружений), то с достаточной для практических целей точностью можно принять отрезок прямой кl компрессионной кривой (рис. 9) за прямую. Тогда согласно обозначениям на рисунке будем имеет
ei = e0 – tgαpi (20)
Тангенс угла наклона отрезка компрессионной кривой к оси давлений tgα характеризует сжимаемость грунта в рассматриваемом диапазоне давлений (от p1до p2), так как чем больше угол наклона α, тем больше будет и сжимаемость грунта. Эта величина носит название коэффициента сжимаемости грунта и обозначается m0, т. е.
m0= tgα. (21)
Коэффициент сжимаемости может быть выражен через значения р и е для крайних точек k и l прямолинейного отрезка (рис. 17):
m0 = (e1 – e2)/(p2 – p1) (22)
или, обозначив p2 – p1= p (где р — приращение давлений, или так называемое действующее давление), будем иметь
m0 = (e1 – e2)/p, (23)
т. е. коэффициент сжимаемости равен отношению изменения коэффициента пористости к величине действующего давления.
Подставляя в уравнение (21) вместо tgα величину т0,получим уравнение прямолинейного отрезка компрессионной кривой в виде
ei = e0 – m0 pi. (24)
Для отрезка к’1′ (рис. 17) кривой набухания (разгрузки) точно таким же путем получим
e’I = e’0 – lgα’ p’i, (25)
где tg α’ — коэффициент набухания.
При расчетах осадок уплотнения грунтов часто пользуются величиной так называемого коэффициента относительной сжимаемости mυ, равной
mυ = m0/ (1 + e0). (26)
Физический смысл этого коэффициента установим на основании следующих соотношений.
Из уравнения имеем
e0 – ei= m0 pi (27)
с другой стороны, из выражения
e0 – ei= (1 + e0)si/ h. (28)
Приравнивая правые части (27) и (28) и принимая во внимание выражение mυ = m0/ (1 + e0), получим
mυ = si / hpi, (29)
т. е. коэффициент относительной сжимаемости равен относительной осадке si / h, приходящейся на единицу действующего давления pi.
Таким образом, имеем следующие характеристики сжимаемости грунтов: Сс, т0и mυ, причем первый коэффициент — число отвлеченное, а коэффициенты т0и тυимеют размерность, обратную удельному давлению (см2/кгс).
Закон уплотнения. Уравнение (24) описывает изменение коэффициента пористости лишь для спрямленного участка компрессионной кривой и поэтому является уравнением приближенным. Если же изменения давлений будут бесконечно малыми, то изменения коэффициента пористости будут строго (точно) пропорциональны изменению давления. Дифференцируя уравнение (24), получим
de = — m0dp. (30)
Полученное соотношение имеет особо важное значение в механике грунтов и кладется в основу установления ряда ее фундаментальных положений: принципа линейной деформируемости, принципа гидроемкости, дифференциального уравнения консолидации и др. и называется законом уплотнения грунтов.
Этот закон формулируется следующим образом: бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления.
При небольших изменениях давлений уравнение (30) можно распространить и на конечные изменения величин е и р. По рис. 17
e1 – e2= m0(p2 – p1). (31)
Тогда закон уплотнения может быть сформулирован следующим образом: при небольших изменениях уплотняющих давлений изменение коэффициента пористости прямо пропорционально изменению давления.
Общий случай компрессионной зависимости.Изменения коэффициента пористости е грунта при компрессионном сжатии в общем случае будут зависеть не только от величины вертикальных нормальных напряжений σz, но и от горизонтальных σy и σx.
Следуя проф. Н. М. Герсеванову, примем наиболее простое положение о том, что коэффициент пористости в любой точке грунтовой массы зависит только от суммы всех нормальных напряжений Θ, действующих в этой точи. Это положение является известным допущением, так как для очень вязких и плотных глинистых грунтов на изменения коэффициента пористости будут в некоторой мере влиять и сдвигающие (касательные) напряжения, обусловливаюшие ползучесть скелета грунта.
Рис. 18. Схема напряжений в элементе грунта при действии сплошной равномерно распределенной нагрузки
Для «грунтовой же массы» в нашем определении, к которой мы относим все полностью водонасыщенные неуплотненные грунты (мелкие пески и супеси, слабые суглинки и глины) с несжимаемым минеральным скелетом и наличием свободной (несвязанной) воды, это положение будет достаточно хорошо отвечать действительности.
Определим сумму главных напряжений в случае сжатия слоя грунта без возможности его бокового расширения, выделив элементарный параллелепипед (рис. 10), который в условиях данной задачи будет испытывать лишь нормальные (главные) напряжения σx, σy и σz.
Так как горизонтальные деформации (расширение грунта в стороны) невозможны, то горизонтальные относительные деформации будут равны нулю, т. е. εx = εy = 0, откуда вытекает, что σx = σy.Кроме того, из условия равновесия имеем σz = p.
Напишем известное выражение для горизонтальной относительной деформации εxпри действии напряжений по трем взаимно перпендикулярным направлениям:
εx = σx / Eо – μо(σy + σz)/ Eо (32)
где Еои μо — модули деформируемости грунта, аналогичные модулю упругости и коэффициенту Пуассона упругих тел, но относящиеся к общей деформации грунта, что отмечено буквой «о».
Подставляя в выражение (32) σx= y, σz=p и εx=0, получим
σx=σy=μоp/ (1 – μо), (33)
или
σx=σy=ξ0p, (34)
где
ξ0=μо / (1 – μо). (35)
Величина ξ0 называется коэффициентом бокового давления грунта в состоянии покоя.
Пользуясь полученными соотношениями, можем составить сумму нормальных напряжений, которую обозначим Θ:
Θ = σx + σy + σz. (36)
Так как σz=p, а σx=σy=ξ0p, то получим
Θ = (1 +2ξ0)p,
откуда
p = Θ / (1 + 2ξ0). (37)
Подставив полученное выражение в уравнение прямолинейного отрезка компрессионной кривой (24), будем иметь
ei= e0 – m0Θ / (1 + 2ξ0), (38)
откуда
ei + m0Θ / (1 + 2ξ0)=e0=const. (39)
Рис. 19 Определение эквивалента капиллярного давления по главной ветви компрессионной кривой
Полученное уравнение показывает, что изменение коэффициента пористости (или влажности) грунтовой массы в данной точке может произойти лишь при изменении суммы главных напряжений Θ в этой точке или, по Н. М. Герсеванову, «гидроемкости» грунтовой массы. Последнее и формулирует так называемый принцип гидроемкости» проф. Н. М. Герсеванова.
Как пример применения принципа гидроемкости отметим способ определения эквивалента капиллярного давления, т. е. величины среднего всестороннего давления рk, заменяющего действие всех капиллярных сил.
По компрессионной кривой образца грунта нарушенной структуры, называемой главной ветвью компрессионной кривой (рис. 19), определяем величину уплотняющего давления, которое может привести грунт из текучего состояния в состояние данной плотности е. Обозначим это давление ps.
При всестороннем сжатии элемента грунтовой массы капиллярным давлением ркего гидроемкость будет равна
Θ=σx +σy+σz =3pk. (40)
С другой стороны, согласно формуле (37)
Θ=(1 +2ξ0)p (41)
Приравнивая правые части выражений (40) и (41), получим
pk=(1+2ξ0)ps/3. (42)
Рис. 20 Влияние бокового давления грунта по результатам опытов: 1 – совершенно рыхлый песок; 2 – уплотненный песок; 3 – водонасыщенный суглинок
Отметим, что изложенный способ определения эквивалента капиллярного давления применим для общей оценки среднего капиллярного давления глинистых грунтов, образовавшихся лишь при гравитационном уплотнения их в водных бассейнах без возникновения жестких цементационных связей.
Для грунтов, не обладающих жесткими связями, если известна высота капиллярного поднятия (всасывания) в них воды hк, т. е. расстояние от уровня грунтовых вод до уровня поверхности капиллярных менисков, капиллярное давление будет равно
pк = γωhк. (43)
Коэффициент бокового давления. В общем случае коэффициент бокового давления грунтов ξ есть отношение приращения горизонтального давления грунта dq к приращению действующего вертикального давления dp, т. е.
ξ=dq/dp. (44)
Отделяя переменные и интегрируя, получим
q=ξp+D. (45)
Выражение (45) есть уравнение прямой с угловым коэффициентом ξ и постоянной интегрирования D,определяемой из начальных условий.
Как показывают соответствующие опыты (В. Г. Булычева, Н. В. Лалетина, К. Терцаги и др.), для весьма рыхлых песков, совершенно не обладающих структурной прочностью, начальное давление (рис. 20) q0=0 и D=0; для предварительно уплотненных песков величина q0 ≠ 0 и составляет некоторую долю от уплотняющего давления р0,т. е. D=q0=αp0 (причем, α<1), а для связных глинистых грунтов оно будет отрицательно и, по Герсеванову, равно капиллярному давлению, т. е. D=- pк, что и подтверждается опытом — прямая 3 на рис. 20 отсекает на оси р некоторый отрезок, равный — pк / ξ.
Значения коэффициента бокового давления ξ получены следующие: для песчаных грунтов ξ=0,25÷0,37 и для глинистых (в зависимости от консистенции) ξ=0,11÷ ,82.
Похожие статьи:
poznayka.org
Сжимаемость грунтов (закон уплотнения).
Сжимаемость грунтов – способность их уменьшаться в объеме (давать осадку) под действием внешнего давления. Степень сжимаемости грунтов зависит от структуры грунта и является важной характеристикой механических свойств грунта, которая используется для расчета осадок зданий и различных сооружений. Сжимаемость грунтов обусловлена изменением их пористости при приложении нагрузки и происходит за счет возникновения взаимных сдвигов частиц. Уменьшения толщины водно-коллоидных пленок отжатия воды в водонасыщенных грунтах и за счет разрушения кристаллизационных связей в сильно структуированных грунтах. В связи с тем, что сжимаемость грунтов связана с уменьшением их пористости, в механике грунтов принято характеризовать сжимаемость грунта зависимостью коэффициента пористости е от уплотняющего давления Р. Эта зависимость называется компрессионной и определяется в лабораторных условиях экспериментально в приборах двух типов: -одометре(приборе одноосного сжатия с жесткими боковыми стенками обоймы, в которую заключен образец грунта) называемым также компрессионным прибором; -стабилометре (приборе трехосного сжатия с эластичными боковыми стенками, в которые заключен грунт).
При относительно малых давлениях < сжимаемость грунта м.б. сравнительно небольшой, значительно меньшей, чем при больших давлениях.
При изменении давления в практических целях заменяют зависимость между Е и Р прямолинейной, т.е. заменяют кривую
на этом участке отрезком стягивающей хорды. Тогда из геометрических соображений получим ,
коэффициент сжимаемости . Для расчета осадок удобнее пользоваться коэффициентом относительной сжимаемости
.Эти показатели необходимы для расчета осадок фундамента зданий или сооружений.
Сформулируем закон уплотнения. Уравнение (1) описывает изменение коэффициента пористости только для спрямленного участка компрессионной кривой и поэтому является приближенным. Но если изменения давлений будут бесконечно малыми, то изменения коэффициента пористости будут точно пропорциональны изменению давления:
Полученное соотношение называется законом уплотнения грунтов: бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления
24.Сопротивление несвязных и связных грунтов сдвигу (закон Кулона).
Грунты оснований зданий и сооружений испытывают воздействие не только нормальных, но и касательных напряжений. Когда касательные напряжения по какой-либо поверхности в грунте достигают его предельного сопротивления, то происходит сдвиг одной части массива грунта по другой.
Сопротивлений грунта сдвигу характеризуется его прочностными свойствами и используется в расчетах оснований по первому предельному стоянию (прочности).
Прочностью грунта называют способность его воспринимать силы внешнего воздействия, не разрушаясь. Прочность грунта определяется его сопротивляемостью сдвигу и оценивается показателем, который называется предельным сопротивлением сдвигу .
Внутренним сопротивлением, препятствующим сдвигу частиц, в песчаных грунтах будет лишь трение, возникающее в точках контакта частиц. В связных же грунтах перемещению частиц будут сопротивляться внутренние структурные связи.
Предельное сопротивление грунтов сдвигу может быть установлено по испытанию его образцов на прямой плоскостной срез, трехосное сжатие, по результатам среза грунта крыльчаткой и др. способами. При испытаниях на прямой плоскостной срез используют односрезный прибор. При этом цилиндрический образец грунта помещают в срезыватель так, чтобы одна его половина оставалась неподвижной, а другая могла перемещаться горизонтально под действием сдвигающей нагрузке. К образцу прикладывается так же вертикальная сжимающая нагрузка.
Рис.10. Схема сдвигового прибора.
Многочисленными экспериментами установлено, что график зависимости предельного сопротивления сдвигу сыпучих грунтов от давления представляет собой прямую, исходящую из начала координат и наклоненную под углом φ к оси давлений.
Рис.11. График сопротивления сдвигу сыпучего грунта.
Эта зависимость может быть выражена уравнением:
,
где φ – угол внутреннего трения грунта.
Это и есть закон Кулона для сыпучих грунтов (1773 г.) — предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.
Основными видами испытаний связных грунтов на сдвиг будут испытания по закрытой (неконсолидированные испытания) и открытой (консолидированные) системам. Испытания грунтов по первой схеме выполняются таким образом, что плотность и влажность грунта в процессе опыта не меняются, и поэтому такие опыты носят название быстрого сдвига. Испытания по открытой схеме производят после предварительного уплотнения образцов вертикальной нагрузкой до стабилизации осадки, а горизонтальное усилие на образец передается ступенями, при этом каждая ступень выдерживается до стабилизации горизонтальной деформации. Испытания сыпучих грунтов производят по первой схеме, а связных по второй.
Диаграмма испытания глинистых грунтов на сдвиг приведена на рис.12.
Рис.12. График сопротивления сдвигу связного грунта.
Опыты показывают, что диаграмму консолидированного сдвига глинистых грунтов, несмотря на кривизну начального участка, без особых погрешностей можно описать уравнением прямой линии:
.
Это уравнение выражает закон Кулона для связных грунтов: предельное сопротивление связных грунтов сдвигу при завершенной консолидации есть функция первой степени от нормального давления.
Т.о. для связных грунтов сопротивление сдвигу характеризуется двумя параметрами: углом внутреннего трения φ и удельным сцеплением с. Если прямую аb продлить влево до пересечения с осью абсцисс, то она отсечет на ней отрезок рε. Величину рε – называют давлением связности. Используя это давление, параметр сцепления (связности) грунта можно представить в виде:
.
Характеристики сопротивления грунтов сдвигу могут быть так же определены по результатам опытов на трехосное сжатие. Прибор для таких испытаний называется – стабилометром.
Т.о., для расчета оснований зданий и сооружений необходимо определить вышеуказанные прочностные характеристики, а именно: угол внутреннего трения и удельное сцепление грунта.
infopedia.su
Сжимаемость грунтов. Закон уплотнения — МегаЛекции
Сжимаемость грунтовявляется характернейшим их свойством, существенно отличающим грунты от массивных горных пород и других твердых тел, и заключается в способности грунтов изменять (иногда значительно) свое строение (упаковку твердых частиц) под влиянием внешних воздействий (сжимающей нагрузки, высыхания, коагуляции коллоидов и пр.) на более компактное за счет уменьшения пористости грунта.
Уменьшение пористости грунтов при более компактной упаковке частиц происходит как вследствие возникновения некоторых местных сдвигов частиц и соскальзывания более мелких частиц в поры грунта, так (особенно у дисперсных водонасыщенных глинистых грунтов) и вследствие изменения толщины водно-коллоидных оболочек минеральных частиц под влиянием увеличения давления, высыхания, коагуляции и пр.
Кроме того, на переупаковку частиц влияет ползучесть скелета грунта и оболочек прочносвязанной воды (которые также можно относить к скелету грунта), обусловленная искажением формы кристаллических решеток минеральных частиц и медленным вязким течением молекулярных слоев прочносвязанной воды.
Следует здесь же отметить, что для грунтов полностью водонасыщенных изменение пористости возможно лишь при изменении их влажности (выдавливании или всасывании воды) и некоторого внутри-объемного сжатия газовых включений; для грунтов же неводонасыщенных оно может происходить и при сохранении их влажности.
Изменение объема пор дисперсных грунтов при высыхании (в процессе обезвоживания диффузных оболочек и увеличения капиллярного сжатия), а также в результате медленных физико-химических процессов (например, старения коллоидов) учитывают лишь в отдельных исключительных случаях, и основным процессом изменения объема грунтов будет уплотнение их под нагрузкой.
Следует различать уплотняемость грунтов при кратковременном действии динамических нагрузок (механическую) и уплотнение при длительном действии постоянной статической нагрузки (компрессию, консолидацию и пр.).
При механическом воздействии вибрационными, трамбующими и подобными механизмами хорошо уплотняются лишь маловлажные рыхлые песчаные и неводонасыщенные грунты, имеющие жесткие контакты между минеральными частицами, которые при этих воздействиях легко нарушаются, что и обусловливает перегруппировку частиц и более плотную их упаковку. В водонасыщенных же песках динамические нагрузки вызывают значительные напоры в воде, грунт взвешивается в некоторой области и при определенных условиях разжижается, растекаясь по большой площади. Однако чем больше внешнее давление на поверхность грунта, подвергаемого динамическому воздействию (например, вибрационному), тем менее оно эффективно, так как труднее преодолеваются усилия в точках контакта частиц.
В глинистых грунтах, которые вследствие их связности при динамических нагрузках уплотняются очень мало, возникающие в воде напоры при незначительной водопроницаемости этих грунтов погашаются на весьма малом расстоянии и разжижения не происходит.
При уплотнении грунтов сплошной постоянной нагрузкой (компрессии грунтов) следует рассматривать, по крайней мере, два диапазона давлений: 1 — когда внешнее давление меньше прочности структурных связей и 2 — когда эти связи преодолены.
В первом случае, как показывают исследования, проведенные в МИСИ и других исследовательских организациях, уплотнения грунтов не происходит, так как возникающие под действием внешней нагрузки деформации в этом случае будут упругими деформациями структурных связей и грунт будет деформироваться как сплошное квазитвердое тело.
Во втором случае, т. е. когда жесткие структурные связи преодолены (при давлениях, больших структурной прочности), грунты будут уплотняться значительно, причем для грунтов с водно-коллоидными связями уплотнение будет происходить за счет сжатия водно-коллоидных оболочек минеральных частиц с выдавливанием некоторого количества воды, а также в известной мере и за счет ползучести скелета грунта. Выдавливание же воды для данных глинистых грунтов возможно лишь при напоре, вызываемом действием внешней нагрузки, большем некоторой начальной величины.
Для грунтов, обладающих одновременно и мягкими водно-коллоидными и жесткими кристаллизационными связями, процесс уплотнения будет значительно сложнее.
Зависимость между влажностью, давлением и коэффициентом пористости. Для установления основных показателей сжимаемости грунта производят испытания его на уплотнение под нагрузкой в условиях одномерной задачи, когда деформации грунта могут развиваться только в одном направлении и никакие другие силы, кроме внешней нагрузки, не действуют.
При испытании водонасыщенного грунта его поверхность покрывают слоем воды, что позволяет избежать высыхания грунта в процессе опыта (который длится обычно от нескольких часов до нескольких дней), а следовательно, избежать развития в нем сил капиллярного давления.
Для испытания грунта на сжимаемость применяют приборы с жесткими стенками (одометры) для обеспечения сжатия грунта только в одном направлении (без возможности его бокового расширения – рис. 13, а).
Рис. 13. Схемы компрессионного сжатия грунта в жестком кольце (а) и при сплошной нагрузке (б)
Подобные граничные условия соответствуют в натуре сжатию отдельного слоя грунта под действием сплошной равномерно распределенной нагрузки (например, веса вышележащих слоев грунта — рис. 13, б). Нагрузку на поверхность грунта прикладывают отдельными возрастающими ступенями (например, 0,05; 0,10; 0,25; 0,5; 1,0; 2,0; 4,0 кгс/см2, соответственно 0,005; 0,010; 0,025; 0,05; 0,1; 0,2; 0,4 МПа), так как чем более будет уплотнен грунт предыдущей ступенью нагрузки, тем меньше будут его деформации и требуется большая точность измерений.
Опытами (проф. Терцаги и др.) было установлено, что для водонасыщенных, но маловодопроницаемых глинистых грунтов каждому приращению внешнего давления соответствует вполне определенное изменение влажности. Зависимость между влажностью и давлением можно изобразить в виде графика (рис. 14, а), который носит название компрессионной кривой. Так как для полностью водонасыщенных грунтов существует закономерная связь между влажностью и коэффициентом пористости [зависимость e = ωmaxγs], то компрессионную кривую (рис. 14, а) легко перестроить в координатах коэффициент пористости — давление (рис. 14, б).
Дальнейшие исследования показали, что компрессионные кривые применимы для оценки сжимаемости любых дисперсных материалов (связных, сыпучих), но для материалов водопроницаемых (например, песков) не могут быть построены по изменению влажности, так как при нагрузке этих материалов влажность восстанавливается почти мгновенно.

Рис. 14. Компрессионные кривые для глинистого грунта: 1 – кривые уплотнения; 2 – кривые разуплотнения (набухания)
Более общим методом построения компрессионных кривых является метод определения коэффициента пористости по осадкам образца грунта при уплотнении их в компрессионном приборе.
Если обозначить:
e0 — начальный коэффициент пористости грунта;
ei — коэффициент пористости грунта при любой ступени нагрузи;
si — полная осадка образца при данной нагрузке (рi,), измеренная от начала загружения;
Δni — изменение пористости грунта (объема пор) от начала загружения;
h — начальная высота образца грунта,
то, учитывая, что коэффициент пористости есть отношение объема пор к объему твердых частиц, будем иметь
ei = e0 – Δni/m. (15)
Так как для образца грунта, испытываемого без возможности бокового расширения, изменение объема пор Δni — численно равно произведению осадки si на площадь образца F, т. е.
Δni = siF, (16)
а объем твердых частиц во всем объеме грунта, учитывая выражение m = 1/(1 + e),
m = Fh · 1/(1 + e0) (17)
то, подставляя (в2) и (в3) в (в1), получим
ei = e0– (1 + e0)si/ h(1) (18)
Формулой (15) и пользуются для вычисления коэффициентов пористости, соответствующих данным ступеням нагрузки, а по ним строят и всю компрессионную кривую.
В ряде случаев (например, при оценке деформируемости просадочных грунтов и учете нелинейности сжатия при большом диапазоне давлений) в качестве характеристики сжимаемости грунтов применяется и так называемый модуль осадки (предложенный проф. Н. Н. Масловым, 1941) εp = si/h — относительная деформация грунта при данном давлении, выраженная в промиллях (мм/м).
Для грунтов естественной ненарушенной структуры компрессионная кривая имеет два участка (рис. 15): первый — до давлений, не превосходящих структурной прочности грунта рстр, с очертанием, близким к линейному, и очень малыми изменениями коэффициента пористости, и второй — криволинейный, со значительными изменениями коэффициента пористости, что указывает на уплотнение грунта под нагрузкой, превосходящей структурную прочность грунта. При меньших же нагрузках уплотнения грунта не происходит.
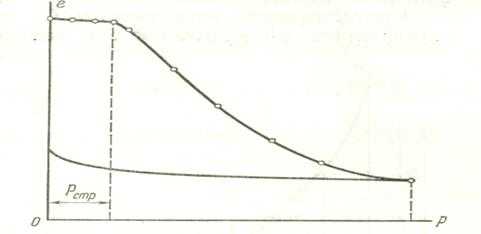
Рис. 15. Компрессионные кривые для образцов грунта ненарушенной структуры
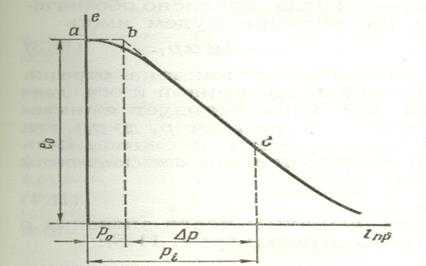
Рис. 16. Компрессионная кривая в полулогарифмических координатах
В дальнейшем мы будем рассматривать компрессионные кривые только при давлениях, больших структурной прочности грунтов.
Что касается величины структурной прочности грунтов рстр, то, как будет показано в последующих главах, она является весьма важной характеристикой грунтов. Величину ее можно определить по компрессионной кривой ненарушенной структуры, испытывая грунты (до достижения структурной прочности) весьма малыми ступенями нагрузки (примерно 0,02-0,10 кгс/см2, 0,002-0,010 МПа), тогда резкий перелом компрессионной кривой и будет соответствовать достижению структурной прочности сжатия грунта (рис. 15).
Другой метод определения структурной прочности предложен проф. Е. И. Медковым по результатам испытания бокового давления грунта при трехосной компрессии и соответствует давлению, при котором практически отсутствует боковое давление грунта.
Определение указанных выше давлений требует разработки специальной методики испытания, и в настоящее время величина структурной прочности может быть определена лишь с известным приближением, зависящим, главным образом, от точности измерений.
Если начертить компрессионную кривую в полулогарифмических координатах (рис. 16), то изменения коэффициента пористости грунта (для давлений, больших структурной прочности) будут линейно зависеть от логарифма изменений внешнего давления. Тогда уравнение компрессионной кривой для большого диапазона давлений может быть представлено в виде
ei = e0 – Сc ln (pi/p0), (19)
где е0и p0 — начальные коэффициент пористости и давление, близкое величине структурной прочности; eiи рi — коэффициент пористости и давление, соответствующее i-й ступени нагрузки; Сс — коэффициент компрессии.

Рис. 17. Определение параметров отрезка компрессионной кривой
Коэффициент компрессии Сс есть тангенс угла наклона полулогарифмической кривой к оси давлений и численно равен разности коэффициента пористости при рi=е, т. е. при pi = 2,72 кгс/см2; (~0,272 МПа) и р0 = 1 кгс/см2, так как при
pi = е lnpi= 1.
Этот коэффициент (по размерности отвлеченное число) характеризует сжимаемость грунтов в большом диапазоне давлений.
Если ограничиться небольшим изменением давлений (порядка 1 — 3 кгс/см2, 0,1 — 0,3 МПа, что обычно и имеет место в основаниях сооружений), то с достаточной для практических целей точностью можно принять отрезок прямой кl компрессионной кривой (рис. 9) за прямую. Тогда согласно обозначениям на рисунке будем имеет
ei = e0 – tgαpi (20)
Тангенс угла наклона отрезка компрессионной кривой к оси давлений tgα характеризует сжимаемость грунта в рассматриваемом диапазоне давлений (от p1до p2), так как чем больше угол наклона α, тем больше будет и сжимаемость грунта. Эта величина носит название коэффициента сжимаемости грунта и обозначается m0, т. е.
m0= tgα. (21)
Коэффициент сжимаемости может быть выражен через значения р и е для крайних точек k и l прямолинейного отрезка (рис. 17):
m0 = (e1 – e2)/(p2 – p1) (22)
или, обозначив p2 – p1= p (где р — приращение давлений, или так называемое действующее давление), будем иметь
m0 = (e1 – e2)/p, (23)
т. е. коэффициент сжимаемости равен отношению изменения коэффициента пористости к величине действующего давления.
Подставляя в уравнение (21) вместо tgα величину т0,получим уравнение прямолинейного отрезка компрессионной кривой в виде
ei = e0 – m0 pi. (24)
Для отрезка к’1′ (рис. 17) кривой набухания (разгрузки) точно таким же путем получим
e’I = e’0 – lgα’ p’i, (25)
где tg α’ — коэффициент набухания.
При расчетах осадок уплотнения грунтов часто пользуются величиной так называемого коэффициента относительной сжимаемости mυ, равной
mυ = m0/ (1 + e0). (26)
Физический смысл этого коэффициента установим на основании следующих соотношений.
Из уравнения имеем
e0 – ei= m0 pi (27)
с другой стороны, из выражения
e0 – ei= (1 + e0)si/ h. (28)
Приравнивая правые части (27) и (28) и принимая во внимание выражение mυ = m0/ (1 + e0), получим
mυ = si / hpi, (29)
т. е. коэффициент относительной сжимаемости равен относительной осадке si / h, приходящейся на единицу действующего давления pi.
Таким образом, имеем следующие характеристики сжимаемости грунтов: Сс, т0и mυ, причем первый коэффициент — число отвлеченное, а коэффициенты т0и тυимеют размерность, обратную удельному давлению (см2/кгс).
Закон уплотнения. Уравнение (24) описывает изменение коэффициента пористости лишь для спрямленного участка компрессионной кривой и поэтому является уравнением приближенным. Если же изменения давлений будут бесконечно малыми, то изменения коэффициента пористости будут строго (точно) пропорциональны изменению давления. Дифференцируя уравнение (24), получим
de = — m0dp. (30)
Полученное соотношение имеет особо важное значение в механике грунтов и кладется в основу установления ряда ее фундаментальных положений: принципа линейной деформируемости, принципа гидроемкости, дифференциального уравнения консолидации и др. и называется законом уплотнения грунтов.
Этот закон формулируется следующим образом: бесконечно малое изменение относительного объема пор грунта прямо пропорционально бесконечно малому изменению давления.
При небольших изменениях давлений уравнение (30) можно распространить и на конечные изменения величин е и р. По рис. 17
e1 – e2= m0(p2 – p1). (31)
Тогда закон уплотнения может быть сформулирован следующим образом: при небольших изменениях уплотняющих давлений изменение коэффициента пористости прямо пропорционально изменению давления.
Общий случай компрессионной зависимости.Изменения коэффициента пористости е грунта при компрессионном сжатии в общем случае будут зависеть не только от величины вертикальных нормальных напряжений σz, но и от горизонтальных σy и σx.
Следуя проф. Н. М. Герсеванову, примем наиболее простое положение о том, что коэффициент пористости в любой точке грунтовой массы зависит только от суммы всех нормальных напряжений Θ, действующих в этой точи. Это положение является известным допущением, так как для очень вязких и плотных глинистых грунтов на изменения коэффициента пористости будут в некоторой мере влиять и сдвигающие (касательные) напряжения, обусловливаюшие ползучесть скелета грунта.
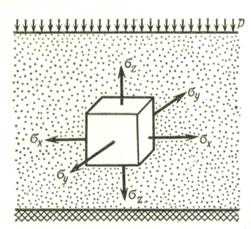
Рис. 18. Схема напряжений в элементе грунта при действии сплошной равномерно распределенной нагрузки
Для «грунтовой же массы» в нашем определении, к которой мы относим все полностью водонасыщенные неуплотненные грунты (мелкие пески и супеси, слабые суглинки и глины) с несжимаемым минеральным скелетом и наличием свободной (несвязанной) воды, это положение будет достаточно хорошо отвечать действительности.
Определим сумму главных напряжений в случае сжатия слоя грунта без возможности его бокового расширения, выделив элементарный параллелепипед (рис. 10), который в условиях данной задачи будет испытывать лишь нормальные (главные) напряжения σx, σy и σz.
Так как горизонтальные деформации (расширение грунта в стороны) невозможны, то горизонтальные относительные деформации будут равны нулю, т. е. εx = εy = 0, откуда вытекает, что σx = σy.Кроме того, из условия равновесия имеем σz = p.
Напишем известное выражение для горизонтальной относительной деформации εxпри действии напряжений по трем взаимно перпендикулярным направлениям:
εx = σx / Eо – μо(σy + σz)/ Eо (32)
где Еои μо — модули деформируемости грунта, аналогичные модулю упругости и коэффициенту Пуассона упругих тел, но относящиеся к общей деформации грунта, что отмечено буквой «о».
Подставляя в выражение (32) σx= y, σz=p и εx=0, получим
σx=σy=μоp/ (1 – μо), (33)
или
σx=σy=ξ0p, (34)
где
ξ0=μо / (1 – μо). (35)
Величина ξ0 называется коэффициентом бокового давления грунта в состоянии покоя.
Пользуясь полученными соотношениями, можем составить сумму нормальных напряжений, которую обозначим Θ:
Θ = σx + σy + σz. (36)
Так как σz=p, а σx=σy=ξ0p, то получим
Θ = (1 +2ξ0)p,
откуда
p = Θ / (1 + 2ξ0). (37)
Подставив полученное выражение в уравнение прямолинейного отрезка компрессионной кривой (24), будем иметь
ei= e0 – m0Θ / (1 + 2ξ0), (38)
откуда
ei + m0Θ / (1 + 2ξ0)=e0=const. (39)
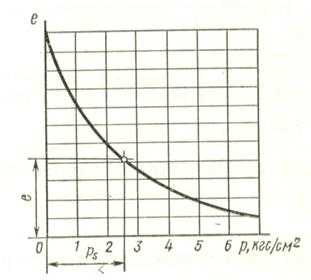
Рис. 19 Определение эквивалента капиллярного давления по главной ветви компрессионной кривой
Полученное уравнение показывает, что изменение коэффициента пористости (или влажности) грунтовой массы в данной точке может произойти лишь при изменении суммы главных напряжений Θ в этой точке или, по Н. М. Герсеванову, «гидроемкости» грунтовой массы. Последнее и формулирует так называемый принцип гидроемкости» проф. Н. М. Герсеванова.
Как пример применения принципа гидроемкости отметим способ определения эквивалента капиллярного давления, т. е. величины среднего всестороннего давления рk, заменяющего действие всех капиллярных сил.
По компрессионной кривой образца грунта нарушенной структуры, называемой главной ветвью компрессионной кривой (рис. 19), определяем величину уплотняющего давления, которое может привести грунт из текучего состояния в состояние данной плотности е. Обозначим это давление ps.
При всестороннем сжатии элемента грунтовой массы капиллярным давлением ркего гидроемкость будет равна
Θ=σx +σy+σz =3pk. (40)
С другой стороны, согласно формуле (37)
Θ=(1 +2ξ0)p (41)
Приравнивая правые части выражений (40) и (41), получим
pk=(1+2ξ0)ps/3. (42)
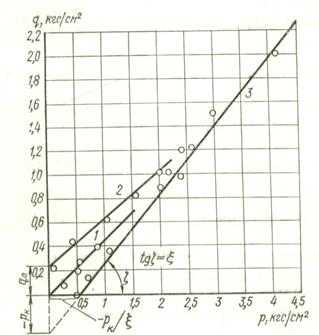
Рис. 20 Влияние бокового давления грунта по результатам опытов: 1 – совершенно рыхлый песок; 2 – уплотненный песок; 3 – водонасыщенный суглинок
Отметим, что изложенный способ определения эквивалента капиллярного давления применим для общей оценки среднего капиллярного давления глинистых грунтов, образовавшихся лишь при гравитационном уплотнения их в водных бассейнах без возникновения жестких цементационных связей.
Для грунтов, не обладающих жесткими связями, если известна высота капиллярного поднятия (всасывания) в них воды hк, т. е. расстояние от уровня грунтовых вод до уровня поверхности капиллярных менисков, капиллярное давление будет равно
pк = γωhк. (43)
Коэффициент бокового давления. В общем случае коэффициент бокового давления грунтов ξ есть отношение приращения горизонтального давления грунта dq к приращению действующего вертикального давления dp, т. е.
ξ=dq/dp. (44)
Отделяя переменные и интегрируя, получим
q=ξp+D. (45)
Выражение (45) есть уравнение прямой с угловым коэффициентом ξ и постоянной интегрирования D,определяемой из начальных условий.
Как показывают соответствующие опыты (В. Г. Булычева, Н. В. Лалетина, К. Терцаги и др.), для весьма рыхлых песков, совершенно не обладающих структурной прочностью, начальное давление (рис. 20) q0=0 и D=0; для предварительно уплотненных песков величина q0 ≠ 0 и составляет некоторую долю от уплотняющего давления р0,т. е. D=q0=αp0 (причем, α<1), а для связных глинистых грунтов оно будет отрицательно и, по Герсеванову, равно капиллярному давлению, т. е. D=- pк, что и подтверждается опытом — прямая 3 на рис. 20 отсекает на оси р некоторый отрезок, равный — pк / ξ.
Значения коэффициента бокового давления ξ получены следующие: для песчаных грунтов ξ=0,25÷0,37 и для глинистых (в зависимости от консистенции) ξ=0,11÷ ,82.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
1. Сжимаемость грунтов. Закон уплотнения
Так как грунт состоит из твердых частиц и пор, которые частично или полностью заполнены водой, теоретически при его сжатии должны уменьшаться объемы всех трех компонентов: твердых частиц, воздуха (газа) и воды. Поскольку напряжения сжатия, возникающие обычно в основаниях сооружений, сравнительно небольшие, объемные деформации твердых частиц, состоящих из таких материалов, как кварц и полевой шпат и др., ничтожно малы и не учитываются. Следовательно, можно считать, что изменение объема грунта при сжатии происходит только из-за изменения объема пор.
Вследствие упругих деформаций скелета (частиц) грунта, тонких пленок воды, расположенных между частицами, упругого сжатия пузырьков воздуха, а также сжатия поровой воды, содержащей растворенный воздух, могут происходить упругие изменения объема грунта. Такие деформации грунта, как правило, во много раз меньше остаточных. Последние развиваются, когда возникающие в грунте напряжения превышают его структурную прочность. В конечном счете остаточные деформации приводят к уплотнению (уменьшению пористости) грунта.
Деформации уплотнения развиваются в результате сдвигов или смещений отдельных частиц грунта относительно друг друга, а также при разрушении частиц, особенно в точках их контактов. Деформации уплотнения пылевато-глинистых грунтов чаще всего протекают медленно во времени. Это объясняется прежде всего тем, что при уплотнении из пор водонасы-щенного грунта должна быть выдавлена вода, без этого грунт уплотняться не может, так как вода практически не сжимается. Процесс же выдавливания воды из водонасыщенных пылевато-глинистых грунтов вследствие их малой водопроницаемости продолжается длительное время. Медленное развитие деформаций как уплотнения, так и сдвигов обусловливается, кроме того, ползучестью связанной воды, окружающей твердые частицы, и ползучестью самого скелета грунта.
Для большого диапазона изменения давления компрессионная кривая первичного сжатия описывается логарифмической зависимостью
где et — коэффициент пористости при давлении рс, еа — начальный коэффициент пористости грунта; Сс — коэффициент компрессии (параметр кривой!; ро — давление, при котором начинается первичное сжатие грунта.
Продифференцировав выражение, получим
Где Ck — постоянная величина.
Следовательно, при первичном сжатии изменение коэффициента пористости грунта прямо пропорционально изменению давления и обратно пропорционально суммарному давлению. Эту зависимость применяют либо при рассмотрении деформаций очень слабых грунтов, либо при изменении давления в значительных пределах.
Давление в грунте основания промышленных и гражданских зданий и сооружений обычно изменяется в небольших пределах. Чаще всего оно повышается не более чем до 0,3 МПа и в редких случаях до 0,6 МПа. При таких давлениях секущая АВ (см. рис. 2.2, б) близка к кривой, т. е. для расчетов можно пользоваться уравнением (2.3). Продифференцировав его, получим
(2.3)
Поэтому закон компрессии грунта формулируется так: изменение коэффициента пористости грунта прямо пропорционально изменению давления.
Правая часть этого равенства является относительной деформацией грунта. Поскольку для определенного грунта и данного изменения давления величина mg постоянна, относительная деформация грунта прямо пропорциональна давлению. Следовательно, грунт можно считать линейно деформируемым телом.
Однако в ряде случаев это положение приводит к значительным расхождениям между рассчитанными и наблюдаемыми в натуре деформациями. Поэтому в последнее время исследователи стремятся учесть нелинейную зависимость между напряжениями и деформациями.
studfiles.net
Основные закономерности механики грунтов (свойства, закон, показатели и применение).сжимаемость грунтов
Законы устанавливают зависимость между различными параметрами механического состояния грунта:
l между напряжениями и деформациями,
l между предельными касательными и нормальными напряжениями,
l между скоростью фильтрации воды через грунт и градиентом напора.
| Свойство | Закон | Показатели | Применение |
| 1. Деформацион-ные свойства | Закон уплотнения | mv — коэффициент относительной сжимаемости, Eo — модуль общих деформаций | При расчёте оснований по второй группе предельных состояний (по деформациям) |
| 2. Прочностные свойства | Закон Кулона | φ- угол внутреннего трения, с — удельное сцепление | При расчёте оснований по прочности и устойчивости (по I группе предельных состояний) |
| 3.Водопроницаемость | Закон Дарси | kf— коэффициент фильтрации, cv— коэффициент консолидации | Расчёт осадок основания во времени |
Сжимаемость грунтов
l Сжимаемость грунтов – свойство грунтов изменять свой первоначальный объём за счёт перекомпоновки частиц и уменьшения пористости.
Условия испытания грунта в компрессионном приборе:
l Грунт деформируется при невозможности боковых перемещений.
l Деформации частиц очень малы и ими можно пренебречь.
l Избыточная вода в грунте свободно выдавливается из пор и удаляется через отверстия в штампах.
l Объём твёрдых частиц в объеме образца не изменяется(вынос мелкодисперсных частиц вместе с избыточной поровой водой не учитывается
Уменьшение объема образца происходит за счет уменьшения объема пор.
Тоже через коэффициент пористости:
Учитывая, что
Получим:
Данная зависимость позволяет оценить изменение
пористости грунта по мере его уплотнения
Испытание грунтов в условиях компрессионного сжатия. Компрессионная зависимость, закон уплотнения.
Компрессионная кривая – график изменения коэффициента пористости грунта с изменением уплотняющего давления.
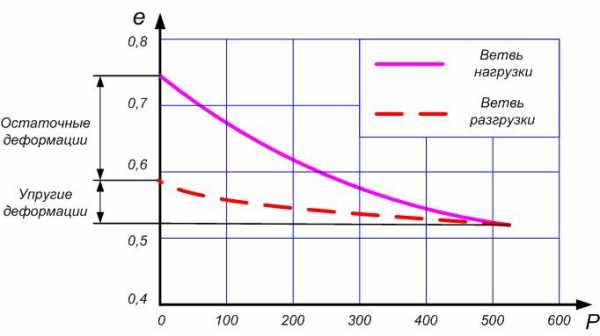
Закон уплотнения
l в ограниченном диапазоне нагрузок зависимость изменения коэффициента пористости от уплотняющего давления есть функция первой степени (линейная функция).
Данная зависимость позволяет оценить изменение
пористости грунта по мере его уплотнения
-(mv) коэффициент относительной сжимаемости
через относительные деформации образца грунта εi.
Компрессивная зависимость при объемном сжатии
megaobuchalka.ru
Сжимаемость грунтов, закон уплотнения — КиберПедия
1. Вопрос: Компрессионная кривая соответствует графику… (где е – коэффициент пористости; р – уплотняющее давление).
Ответ: 1. 4
2.2
3. 1
4. 3
2. Вопрос: Сжимаемость грунтов определяется с помощью …
Ответ: 1. прибор стандартного уплотнения
2. крыльчатки
3. режущего кольца
4. одометра
3. Вопрос: Компрессионной кривой называется кривая зависимости …
Ответ: 1. осадки грунта от влажности
2. коэффициент пористости от влажности (возможно второе значение)
3. коэффициент пористости от уплотняющего давления
4. осадки грунта от давления
4. Вопрос: При динамических нагрузках хорошо уплотняются …
Ответ: 1. глинистые грунты
2. грунты с водно-коллоидными связями
3. мягкопластичные суглинки
4. рыхлые неводонасыщенные пески
5. Вопрос: Ветвь набухания комперессионной кривой соответствует графику … (где е -коэффициент пористости; е0 – начальный коэффициент пористости; p — давление).
Ответ: 1. 3
2. 4
3. 2
4. 1
6. Вопрос: Закон уплотнения грунта имеет формулировку: при небольших изменениях уплотняющих давлений изменение …
Ответ: 1. осадки грунта прямо пропорционально изменению влажности грунта
2. коэффициента пористости прямо пропорционально изменению влажности грунта
3. коэффициента пористости прямо пропорционально изменению давления
4. пористости грунта прямо пропорционально изменению давления
5. Деформационные характеристики грунтов, их определения
1. Вопрос: Коэффициент относительной сжимаемости mv равен… (где mо – коэффициент сжимаемости грунта; ео – начальный коэффициент пористости; Si – осадка грунта при давлении pi ; h – высота образца грунта).
Ответ: 1.
2.
3.
4.
2. Вопрос: Модуль общих деформаций грунта зависит от … (где β – функция от коэффициента относительной поперечной деформации грунта; mv – коэффициент относительной сжимаемости; е0 – начальный коэффициент пористости; γ – удельный вес грунта; p – давление на грунт).
Ответ: 1. е0 и mv(возможно второе значение)
2. β и γ
3. е0 и W
4. β и mv
3. Вопрос: Деформационной характеристикой грунта является …
Ответ: 1. коэффициент пористости
2. пористость
3. сопротивление грунта сдвигу
4. модуль общей деформации
4. Вопрос: Модуль общей деформации характеризует деформации грунта …
Ответ: 1. упругие и остаточные
2. при набухании
3. при морозном пучении
4. за счет ползучести скелета
5. Вопрос: Модуль общих деформаций грунта Е0 определяется по результатам штамповых испытаний по формуле … (где ν – коэффициент Пуассона; ω – безразмерный коэффициент, зависящий от формы подошвы штампа; d – диаметр штампа; ∆ S – приращение осадки от изменения давления ∆ р).
Ответ: 1. (1 – ν2) · ω·
|
3. (1 – ν2) · ω · d ·
4.
6. Вопрос: Коэффициент пористости грунта еi при компрессионных испытаниях под давлением рi равен … (где е0 – начальный коэффициент пористости; Si – осадка от давления рi; h –высота образца грунта).
Ответ: 1. е0 + (1 — е0) ∙
2. е0 + (1 + е0) ∙
3. е0 — (1 + е0) ∙
4. е0 — (1 — е0) ∙
7. Вопрос: Модуль общей деформации грунта Е0 определяется методом статистического зондирования по формуле … (где F – площадь основания зонда; qс – удельное сопротивление погружения конуса зонда).
|
2.
3. a · qс · F
4. a · F
cyberpedia.su