Кпд полиспаста формула: Расчет полиспаста, расчет КПД

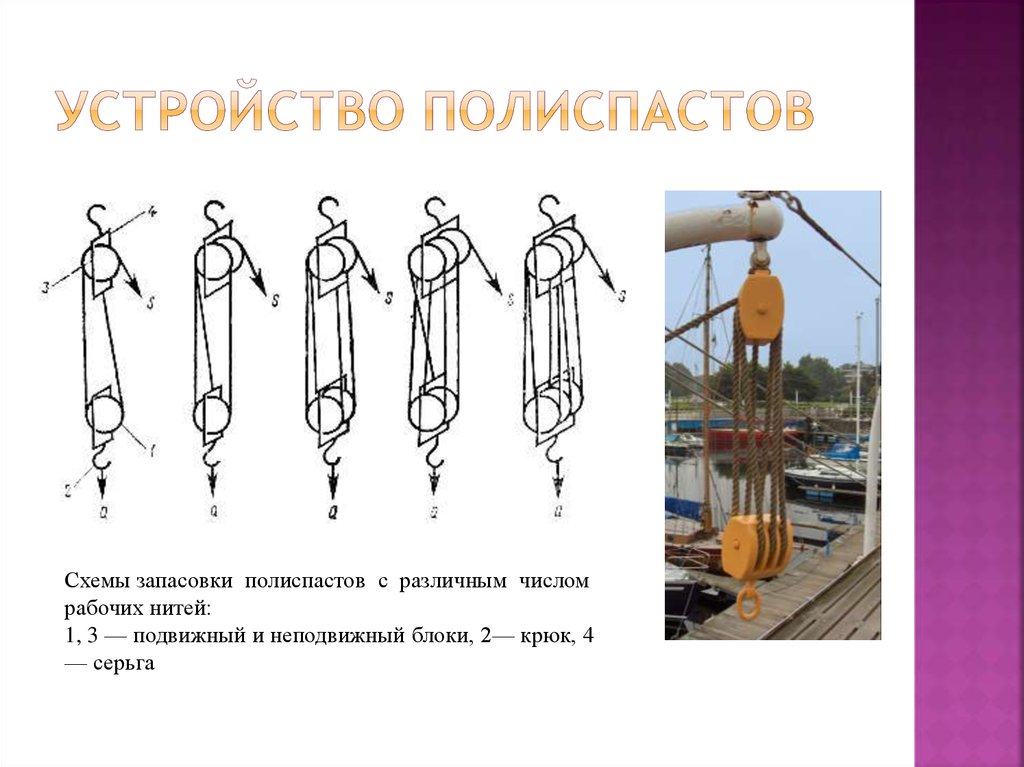
Расчет полиспаста, расчет КПД

Пришло время продолжить цикл статей об оснастке крана. В предыдущей статье про полиспасты были подробно рассмотрены схемы и способы их применения. Но математическая основа полиспаста была затронута крайне мало. Судя по реакции наших читателей — это упущение. Поэтому давайте подробно рассмотрим расчет полиспаста в этой статье.

 

 

 

 

 

Начнем по порядку.

Рассмотрим отдельно взятый блок полиспаста и нагрузки возникающие в нем.

Расчет блока полиспаста

Рисунок 1

• Sн — сила, с которой груз воздействует на блок полиспаста;
• Sс — сила, с которой мотор крана воздействует на блок полиспаста;
• а (альфа) — потенциальный угол отклонения от оси;
• d — диаметр втулки блока полиспаста;
• D — диаметр ручья блока полиспаста.

На основе данной схемы полиспаста составим уравнение моментов сил.

• Sн*R -момент силы воздействия груза;
• q*Sн*R — момент силы необходимой на сгибание и разгибание троса;
• N — нагрузка на ось блока полиспаста;
• f — коэффициент трения втулки полиспаста о блок.

Коэффициент q определяется экспериментально и означает жесткость данного троса при огибании данного ролика полиспаста. Силы, возникающие при набегании и сбегании троса, обусловлены структурой самого троса, а точнее силами трения ниток внутри троса.

Как вы сами понимаете по сравнению с силами трения втулки блока полиспаста необходимое усилие на сгибание и разгибание троса крайне мало. Поэтому рекомендую пока об этом коэффициенте сильно не задумываться.

Теперь найдем нагрузку на ось блока полиспаста. Разницей в нагрузках на набегающей и сбегающей ветках мы пренебрегаем.

Собрав все это воедино, получаем:

Формулу расчета КПД блока полиспаста

Как всегда, КПД показывает отношение выполненной работы к затраченной. Для дальнейших расчетов давайте немного обратимся к практике.

• Первое.

  При прочтении у вас, скорее всего, сразу возник вопрос о каких углах отклонения вообще идет речь? Действительно, современные полиспасты их просто не имеют. В этих углах нет никакого практического смысла. Можно смело заменить синус из формулы на единицу.

• Второе.

  Как уже упоминалось ранее, значение q крайне мало относительно f. В реальных условиях его опускают. Также очень малое значение имеют диаметр ручья полиспаста.

Ну, собственно, у нас остается только сила трения блока полиспаста о его втулку. Таким образом, основное значение при выборе полиспаста имеет качество материалов, из которых он изготовлен, а вернее материалы втулки.

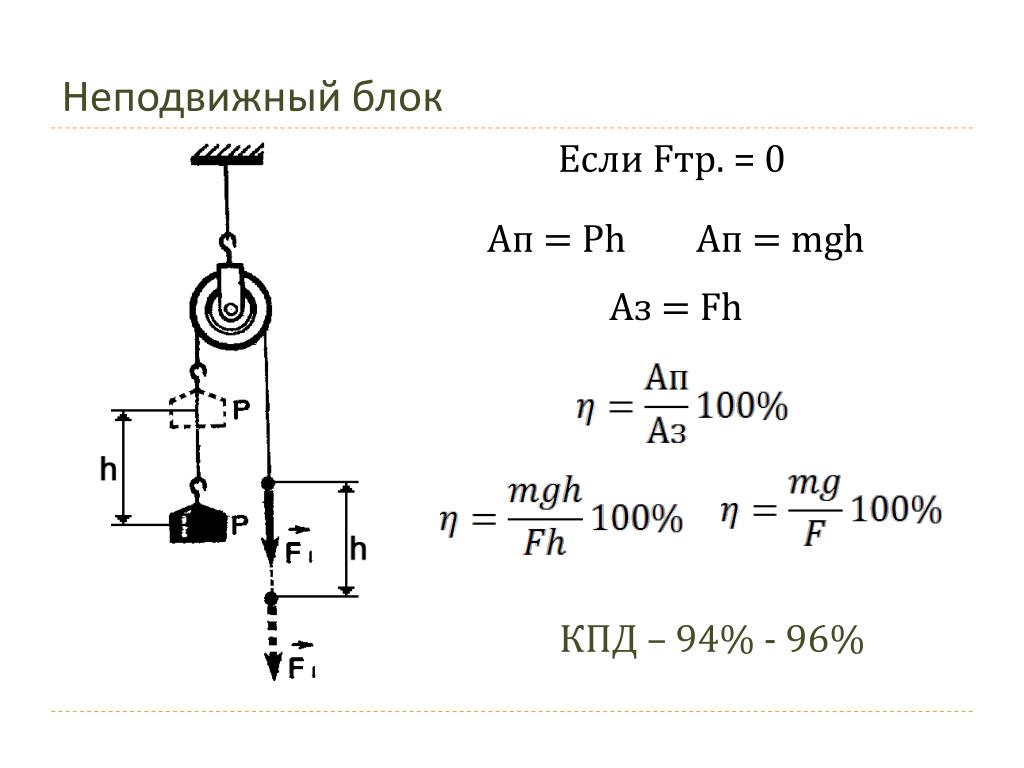
При расчетах используются следующие величины КПД блока полиспаста:

• 100% — недостижимый идеал;
• 97% — среднее значение при использовании бронзовых втулок в подшипниках качения;
• 95% — средние значение при использовании подшипников скольжения;
• 93% и меньше — сильно запыленные места, сильно повышенная температура или агрессивные среды использования.

Не забываем, что мы до сих пор рассматриваем один единственный ролик, а он у нас не один и не два.

Расчет системы силового полиспаста

Рисунок 2

Как видно из рисунка, весь вес груза распределиться равномерно по всем веткам полиспаста и ветке троса идущего на барабан. Но это только в статике, т.е. при отсутствии движения. В динамике картина совсем другая.

При подъеме груза усилие мотора крана, проходя через каждый блок полиспаста, будет уменьшаться из-за потерь на преодоление сил трения внутри блока.  Величина потерь на каждом блоке и есть наш КПД найденный парой абзацев выше. Давайте выразим все нагрузки внутри полиспаста через нагрузку Sо.

Сложив все эти усилия и применив формулы преобразования геометрической прогрессии, мы получим вес груза в зависимости только от Sо. Теперь зная вес груза легко найти нагрузку Sо, а следовательно и параметры(качество) троса необходимого для подъема данного груза с использованием данного полиспаста.

Но это еще не все. Между полиспастом и барабаном подъемного крана обязательно будут располагаться несколько обводных роликов, и самая большая нагрузка ляжет на ветку, идущую от последнего обводного блока к барабану.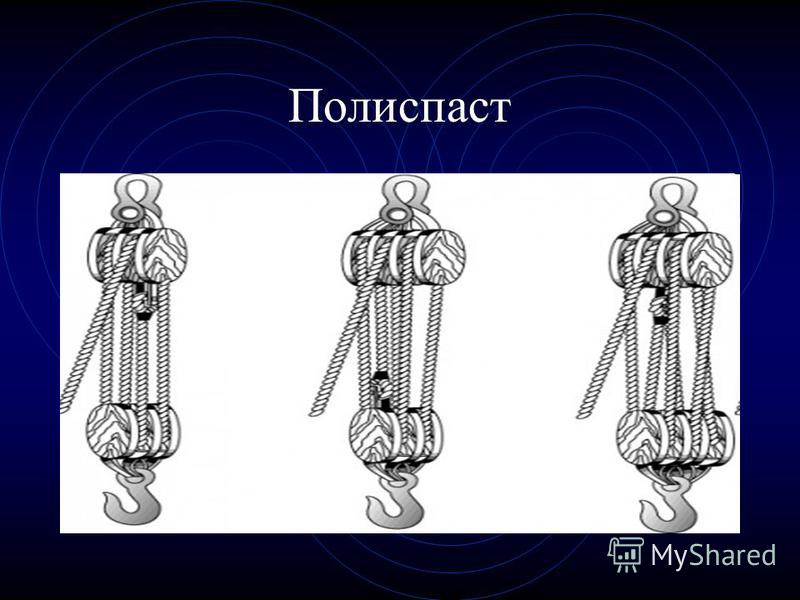

Следовательно, нам необходимо доработать формулу для более точного результата.

• k — общее количество обводных блоков;
• (n+1) — общее количество нитей на которых висит груз.

Вот, собственно, и всё. Зная количество и качество всех роликов в полиспасте, Вы достаточно легко вычислите параметры нужного вам троса.

Внимание! На сайте добавлен сервис расчету основных характеристик полиспаста и параметров троса для запасовки.

Комментировать

Примеры расчета

В.Иванов Примеры предварительного расчета механизмов грузоподъемных кранов

Пример 1. При работе механизма подъема груза на велосипедном кране в цехе металлургического завода наблюдаются рывки при пуске. Выполнить проверочный расчет механизма и предложить простой способ снижения ускорений при пуске (увеличить время пуска).

Исходные данные для расчета:

• грузоподъемность – 1 т;

• скорость подъема груза – 18 м/мин;

• высота подъема – 5 м;

• режим работы – А3.

Расчет механизма подъема. Принимаем плоский полиспаст с кратностью i_п = 2, блоки на подшипниках качения, условия работы нормальные, КПД одного блока η = 0,98 по [4]. Конструкцию крюковой подвески принимаем по [4]. Масса крюковой подвески m_под = 36,4 кг.

Расчетная грузоподъемность

Рисунок 1 – Схема запасовки каната

Максимальное усилие в канате

где – КПД полиспаста;

– табличное КПД полиспаста при i_п = 2;

– КПД направляющих блоков;

j – число направляющих блоков, для велосипедного крана ;

а_п = 1 – для плоского полиспаста.

С учетом коэффициента использования каната z = 3,35 по [3] разрывное усилие

По [5] выбираем канат двойной свивки типа ЛК-Р конструкции 6×19(1+6+6/6)+1 о. с. по ГОСТ 2688-80. Диаметр каната d_к = 6,9 мм, расчетное разрывное усилие каната в целом F_раз = 24,5 кН.

По номинальной грузоподъемности и группе режима работы выбираем крюк однорогий №6, тип А.

Расчет барабана.

Шаг нарезки на барабане

Диаметр барабана по средней линии навитого каната

где h₁ – коэффициент выбора диаметров, принятый равным 14 при легком режиме работы [3].

Из стандартного ряда диаметров барабанов выбираем барабан диаметром равным 0,13 м.

Определяем длину барабана.

Рабочее число витков каната на барабане

где Н – высота подъема груза;

D_Б – диаметр барабана.

Длина барабана l₁ на закрепление каната по [2]

С той стороны, где канат не закрепляется, длина не нарезаемой части

Принимаем 1,5 витка в соответствии с [4] для того, чтобы уменьшить выдергивающую силу каната из-под планки.

Следовательно, полная длина барабана

Получим отношение

т.е. барабан испытывает в основном напряжение на смятие.

Толщина стенки барабана, выполненного из чугуна СЧ18-36, определяется в соответствии с [1] по формуле

где [σ]_см = 90 МПа – допускаемое напряжение для чугуна.

Исходя из технологии отливки, толщина стенки барабана

Принимаем толщину стенки барабана равной 10 мм.

Статическая мощность на подъем груза номинальной массы

По [1] подбираем электродвигатель МТF012-6, номинальная мощность которого при ПВ=15% составляет 3,1 кВт, частота вращения ротора n₁=785 мин^-1, момент инерции J_p=0,029 кг∙м², максимальный развиваемый момент равен 56 Н∙м.

Масса двигателя 58 кг. Габаритные размеры: диаметр 236 мм, длина 450 мм.

Определяем частоту вращения барабана

Необходимое передаточное отношение механизма

Момент на тихоходном валу редуктора

где – КПД передач от барабана до электродвигателя, принимаем равным 0,9;

– КПД барабана, принимаем равным 0,98.

По [1] принимаем крановый редуктор Ц2-250, имеющий передаточное число u_p = 9,8. Масса редуктора 130 кг.

Фактическая скорость подъема груза

Отличия от заданной скорости составляет 9,75%, что допустимо.

Выбор тормоза. Статический момент на первом валу при торможении номинального груза

Расчетный момент для выбора тормоза

где k_T – коэффициент запаса торможения, принимаемый 1,5.

Мы выбираем тормоз ТКГ-160, тормозной момент 100 Н∙м при ПВ= 15% и муфту зубчатую МЗ-1.

Составляем компоновочную схему механизма. Тормоз размещается между электродвигателем и редуктором.

Проверка двигателя на время разгона.

Фактический КПД механизма

Фактическая мощность на подъем номинального груза

Номинальный момент электродвигателя

Статический момент на первом валу с учетом фактического КПД при пуске

где F_k = F_max – подъемная сила в гибком тяговом органе.

Угловая скорость двигателя

Потребное время разгона механизма при подъеме номинального груза

где ω_дв – угловая скорость двигателя;

Т_{П. СР} – средний пусковой момент двигателя;

Т_СТ.Р – момент статических сопротивлений при разгоне, приведенный к валу двигателя;

J_мех.р – приведенный к валу двигателя момент инерции при разгоне всех движущихся частей механизма.

Средний пусковой момент двигателя будет равен

где ψ_П.СР = 1,55 – кратность среднепускового момента.

Момент инерции при разгоне всех движущихся частей механизма будет равен

где – момент инерции поступательно движущихся масс.

Момент инерции при разгоне всех вращающихся частей механизма, приведенных к валу двигателя

где γ = 1,1÷1,2 – коэффициент учета инерции вращающихся масс.

Момент инерции вращающихся масс будет равен

Ускорение, возникающее при разгоне

Для снижения этого ускорения можно увеличить момент инерции вращающихся масс, например, с помощью установки дополнительного диска с моментом инерции 0,3 кг∙м².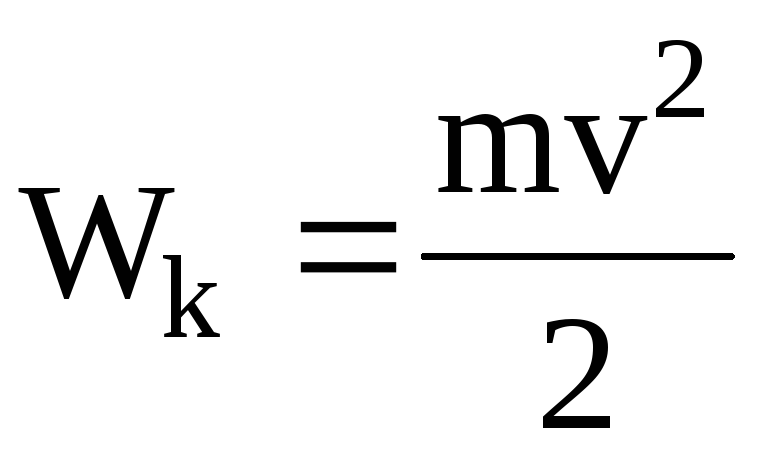 При этом момент J_мех.р = 0,4 кг∙м², t_п = 1,73 с и ускорение a_ф = 0,158 м/с².

Пример 2. На поворотном кране грузоподъемностью 3,2 т производится замена электротали на тележку с канатной тягой. Необходимо рассчитать механизм подъема (выбрать двигатель, редуктор, тормоз, определить основные размеры барабана).

Стрела крана будет выполнена из двух швеллеров, связанных в конце стрелы с помощью листа. Необходимо определить нужный номер швеллера, учитывая только вертикальную нагрузку от веса груза.

Исходные данные для расчета:

• грузоподъемность – 3,2 т;

• скорость подъема груза – 18 м/мин;

• высота подъема – 3,0 м;

• вылет – 3 м;

• режим работы – А4.

1. Составляем схему полиспаста

Рисунок 2 – Полиспаст

2. Определяем к. п.д. системы

К.п.д. полиспаста выбираем по [2, табл.1.2] η_п=0,99.

К.п.д. направляющих блоков находим по формуле

где z_н.бл. – число направляющих блоков, z_{н.бл .}= 5;

η_бл – к.п.д. одного неподвижного блока; η_бл = 0,98.

Общий к.п.д. будет равен

3. Выбор каната

Масса подвески m_подв = 0,05∙m_гр = 0,05∙3,2 = 0,16 т.

Масса груза с подвеской m_расч = m_гр + m_подв = 3,2 + 0,16 = 3,36 т.

Сила тяжести

Натяжение в ветви каната, идущей на барабан

z_k – число ветвей каната, навиваемых на барабан, z_k = 2 (рисунок 2).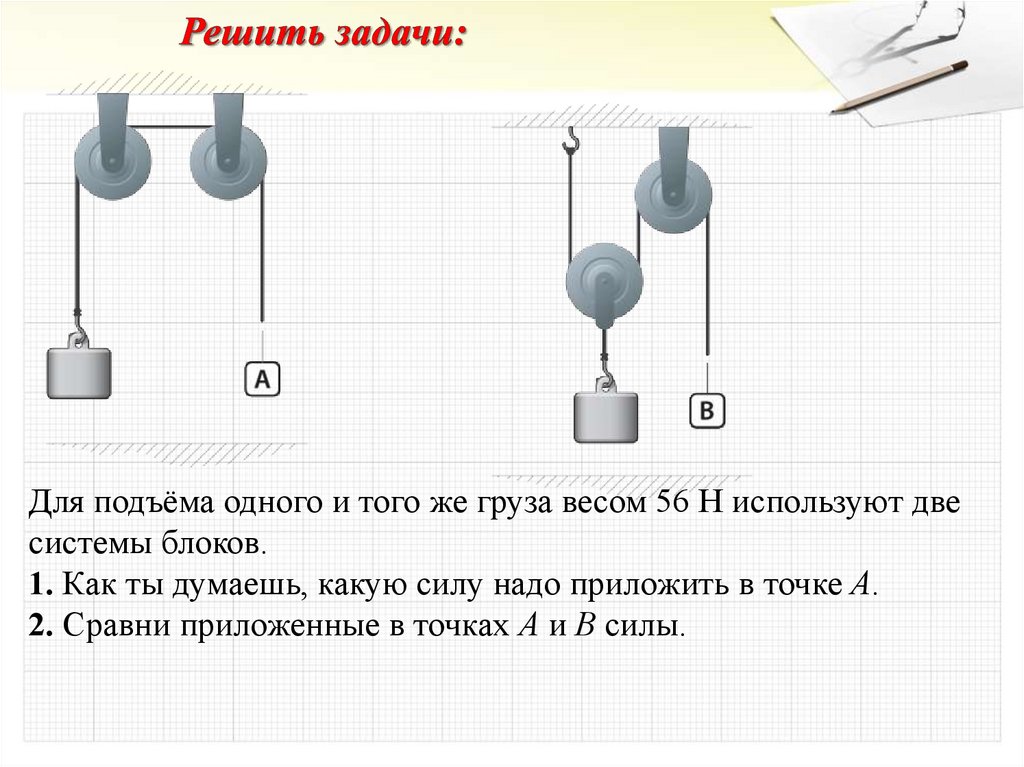

Разрывное усилие в канате

где z_р – минимальный коэффициент использования каната.

Выбираем канат по ГОСТ 2688 ЛК-Р с F_разр = 37750 Н, d_k = 8,3 мм.

4. Выбор крюка

Крюк №12 для среднего режима работы грузоподъемностью четыре тонны.

5. Основные размеры барабана

Шаг нарезки на барабане

Длина одного нарезного участка

где z_p – число рабочих витков;

z_непр – число неприкосновенных витков, z_непр=1,5;

z_кр – число витков для крепления каната, z_кр = 3…4.

где Н – высота подъема груза;

D_Б – диаметр барабана.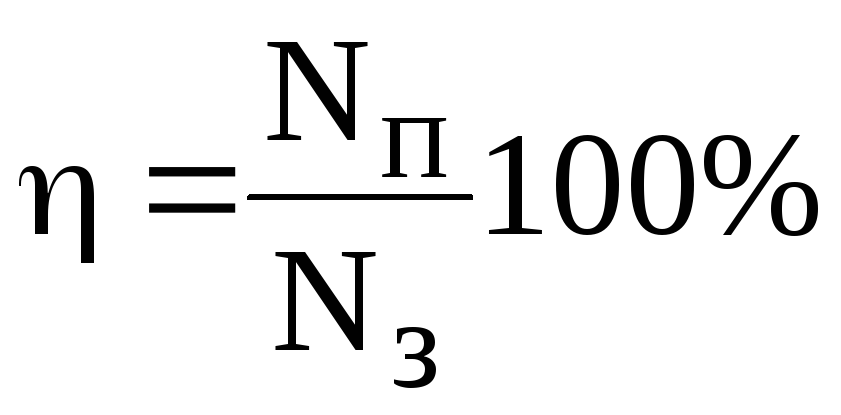

Диаметр барабана по средней линии навитого каната:

где h₁ – коэффициент выбора диаметров.

Из стандартного ряда диаметров барабанов выбираем барабан диаметром равным 150 мм.

Полная длина барабана:

где l₀ – длина гладкого участка, l₀ = 50 мм;

l_k – длина концевого участка, l_k ≈ 50 мм.

Диаметры блока и управляющих блоков соответственно равны

Получим отношение

Для уменьшения изгибающих напряжений и увеличения долговечности каната можно увеличить диаметр барабана.

Принимаем D_Б = 200 мм, тогда

В дальнейших расчетах D_Б = 200 мм.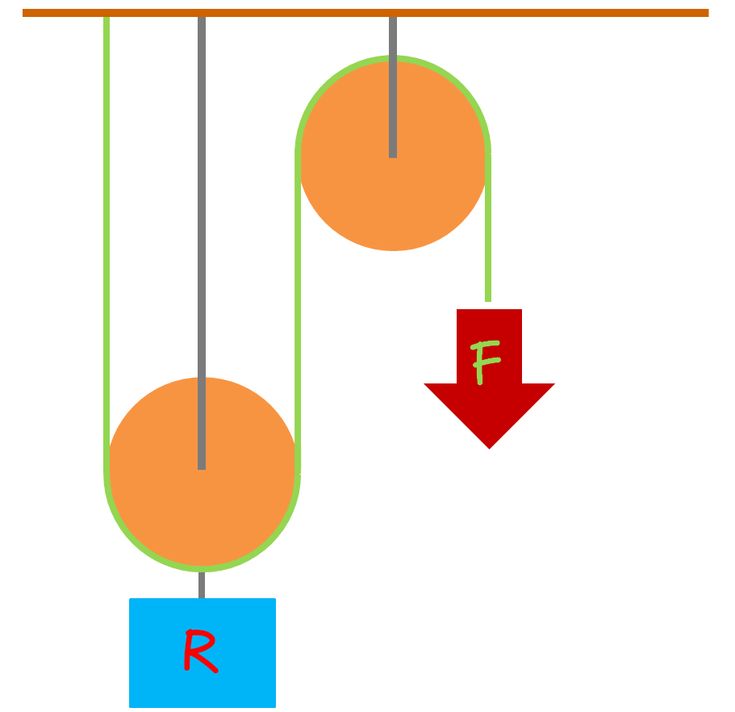

Толщина стенки барабана при F_k = S_max

где [σ]_см = 137,3 МПа – допускаемое напряжение для стали 20.

Исходя из технологии отливки, толщина стенки барабана

С учетом изнашивания можно принять δ_ст=10 мм.

6. Выбор двигателя

Максимальная статическая мощность, которую должен иметь механизм в период установившегося движения при подъеме номинального груза

По [1] подбираем электродвигатель МТF 211-6, номинальная мощность которого при ПВ=25% составляет 9 кВт, частота вращения ротора n₁=915 мин^-1, момент инерции J_p=0,115 кг∙м², максимальный развиваемый момент равен М_max=191 Н∙м.

Номинальный момент

7. Выбор редуктора

Число оборотов барабана

Передаточное число

Момент на тихоходном валу редуктора

Мощность на тихоходном валу редуктора

По [7] выбираем редуктор Ц2-250, имеющий передаточное число u_p = 16.

Фактическая скорость подъема груза

8. Расчет тормозного момента и выбор тормоза

Определяем фактический КПД механизма

Статический крутящий момент при торможении

Тормозной момент

Выбираем тормоз типа ТКТ-200 с тормозным моментом Т_Т = 160 Н∙м и регулируем.

9. Проверка времени пуска

Статический крутящий момент на первом валу при пуске

Потребное время пуска

где ω_дв – угловая скорость двигателя;

Т_П.СР – средний пусковой момент двигателя;

Т_СТ.Р – момент статических сопротивлений при разгоне, приведенный к валу двигателя;

J_{мех. р} – приведенный к валу двигателя момент инерции при разгоне всех движущихся частей механизма.

Средний пусковой момент двигателя будет равен

где ψ_п.ср = 1,6 – кратность среднепускового момента.

Момент инерции масс на первом валу

Момент инерции при разгоне всех вращающихся частей механизма, приведенных к валу двигателя:

где γ = 1,1÷1,2 – коэффициент учета инерции вращающихся масс.

Момент инерции поступательно движущихся масс

Общий момент инерции при разгоне

10. Расчет стрелы

Материал: Сталь 20, σ_Т = 250 МПа.

Требуемый момент сопротивления

Для одного швеллера

Выбираем швеллер №27 с W_x—x = 308 см³.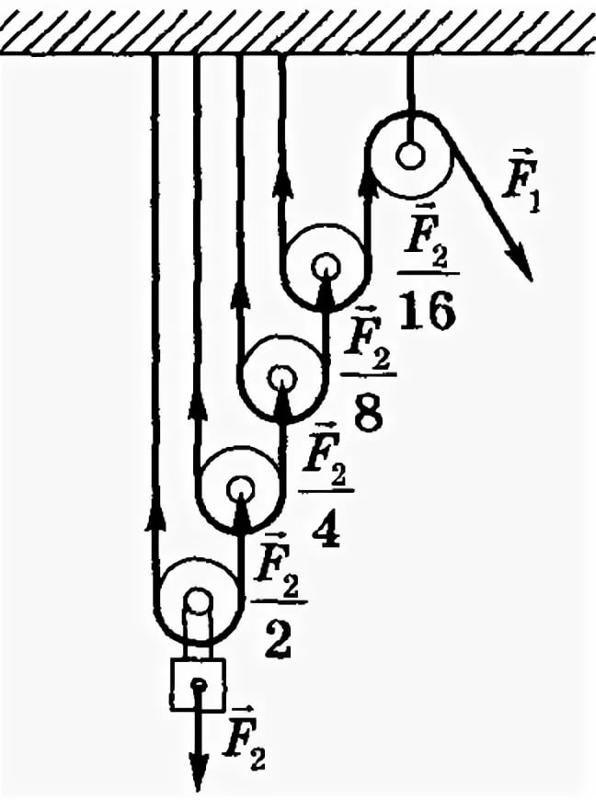

Пример 3. На работающем в цехе мостовом электрическом кране грузоподъемностью 20,0 т вышел из строя двигатель механизма подъема. Необходимо подобрать асинхронный двигатель переменного тока с фазным ротором, учитывая, что на кране установлен барабан диаметром 300 мм и полиспаст, сдвоенный кратностью 2. Кроме того, должны быть выдержаны следующие параметры: высота подъема – 10 м; скорость подъема – 35,0 м/мин; группа режима работы А3.

1. Расчет механизма подъема

Принимаем сдвоенный полиспаст кратностью i_п = 2.

КПД полиспаста η_п =

Сила тяжести груза

Вес подвески G_п=500 Н. Общий вес 196200+500=196700 Н.

Максимальное усилие в канате

Разрывное усилие

Выбираем канат ЛК-Р0 с диаметром канат d_к = 20 мм, расчетным разрывным усилием каната в целом F_раз = 238,5 кН.

По номинальной грузоподъемности и группе режима работы выбираем крюк однорогий №19 ГОСТ6627-74.

2. Расчет барабана

Шаг нарезки на барабане

Диаметр барабана по средней линии навитого каната

где h₁ – коэффициент выбора диаметров, принятый равным 14 при легком режиме работы [3].

Из стандартного ряда диаметров барабанов выбираем барабан диаметром равным 0,3 м.

Рабочее число витков каната на барабане

где Н – высота подъема груза;

D_Б – диаметр барабана.

Длина одного нарезанного участка

где z_p – число рабочих витков;

z_непр – число неприкосновенных витков, z_непр=1,5;

z_кр – число витков для крепления каната, z_кр = 3. ..4.

Полная длина барабана

Принято длина гладкого участка l₀ = 50 мм, концевого l_k = 100 мм.

Диаметры блока и управляющих блоков соответственно равны

Толщина стенки барабана из расчета на сжатие

Сталь 20 → [σ]_см = 137,3 МПа.

Исходя из технологии отливки, толщина стенки барабана

Принимаем толщину стенки барабана равной 20 мм.

Мощность двигателя

С учетом возможности снижения потребной мощности

По [1] подбираем электродвигатель МТН 613-10, номинальная мощность которого составляет 90 кВт, частота вращения ротора n₁=580 мин^-1, момент инерции J_p=6,37 кг∙м², максимальный развиваемый момент равен Т_max=4200 Н∙м.

Номинальный момент двигателя

3. Выбор редуктора

Частота вращения барабана

Передаточное число

Момент на тихоходном валу редуктора

Мощность на тихоходном валу редуктора

По [7, табл.5.30] выбираем редуктор Ц2-400, имеющий передаточное число u_p = 8,32.

Фактическая скорость подъема груза

Отличие от заданной менее 10%.

4. Расчет тормозного момента и выбор тормоза

Определяем фактический КПД механизма

Статический крутящий момент при торможении

Тормозной момент

Выбираем тормоз типа ТКТГ-600.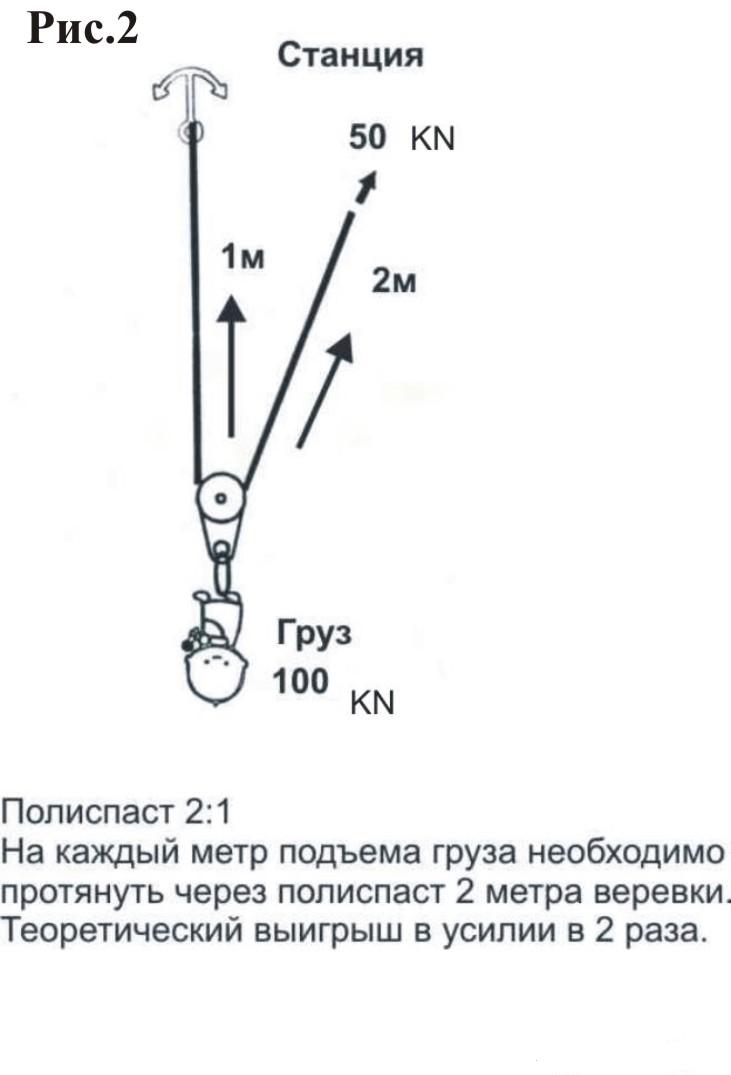

Потребное время разгона

где ω_дв – угловая скорость двигателя;

Т_П.СР – средний пусковой момент двигателя;

Т_СТ.Р – момент статических сопротивлений при разгоне, приведенный к валу двигателя;

J_мех.р – приведенный к валу двигателя момент инерции при разгоне всех движущихся частей механизма.

Средний пусковой момент двигателя будет равен

где ψ_п.ср = 1,6 – кратность среднепускового момента.

Момент инерции масс на первом валу

Как рассчитать эффективность труда

Обновлено 20 сентября 2019 г.

Автор S. Hussain Ather работа вложена в него. Формула эффективности работы поможет вам количественно оценить это и оценить эффективность любой машины.

Формула эффективности работы

Формула для расчета эффективности работы представляет собой соотношение 9От 0011 вывод до ввод , выраженный в процентах. Для машины вы можете определить работу, вложенную в машину, в зависимости от того, как работает машина. Как правило, вы можете рассчитать работу, умножив силу на расстояние для движения.

Убедитесь, что вы правильно рассчитали ввод и вывод машины или объекта, который выполняет работу, а также учитываете другие факторы, такие как человек, управляющий машиной.

Формула эффективности работы эффективность = выход/вход , и вы можете умножить результат на 100, чтобы получить эффективность работы в процентах. Это используется в различных методах измерения энергии и работы, будь то производство энергии или эффективность машины.

Пример расчета эффективности работы

Веревка шкива, которая тянет 10-фунтовый груз на 1 фут от земли из-за того, что человек прикладывает силу 6 фунтов, чтобы потянуть верёвку шкива на 2 фута, имеет указанные входную и выходную силы. Человеческая сила, вложенная сила, выполняет 6 фунтов на 2 фута работы, или 12 футо-фунтов работы. Движение машины, выходная сила, составляет тогда 10 фунтов на 1 фут работы или 10 фут-фунтов работы.

Эффективность работы в этом случае представляет собой отношение выпуска к затратам в процентном выражении. Это будет 10/12 или 0,83. Умножьте это на 100, чтобы перевести в проценты, что даст эффективность работы 83 процента.

Work Efficiency Definition Physics

Отношение объема работы к затратам используется в качестве меры эффективности во многих областях физики и техники. Исследователи считают полезным описывать процент продуктов и расходных материалов для процесса, чтобы определить, как сохранить энергию, мощность или другие ограниченные количества.

Определение отношения выходных данных к входным дает представление о том, насколько эффективна система, процесс, метод, конвейер или что-то еще, что используется.

При анализе термодинамики тепловых двигателей, например, полезная выходная мощность, которую тепловая машина, такая как тепловая машина Карно, может измерять работой, которую двигатель может выполнить в качестве выхода, с высокотемпературным теплом, которое двигатель использует в качестве входа.

Формула эффективности работы на практике

Физики и инженеры используют эффективность работы при определении того, насколько продуктивны и энергосберегающие процессы для электрических цепей (электрический КПД), тепловых двигателей (тепловой КПД), радиоактивных процессов (радиационный КПД), других процессов в том числе квантовая механика (квантовая эффективность).

Простое соотношение вывода и ввода означает, что ученые и инженеры могут использовать свои упрощенные, универсальные математические формулы для любого типа эффективности или цели, в которой они нуждаются. Например, вы можете использовать отношение мощности, излучаемой антенной, к мощности, которую она поглощает на своих терминалах при обнаружении радиочастот, в качестве меры эффективности.

Эффективность чаще выражается в процентах, так как она напрямую сравнивает два фактора: вход и выход. Однако бывают случаи, когда эффективность можно измерить без процентного соотношения, например, 9.0011 удельный импульс , импульс, деленный на массу для ракеты с учетом того, как она использует топливо или топливо, а также сопротивления воздуха и других сил. Удельный импульс дает физикам и инженерам возможность определять тягу, КПД и меры расхода топлива при проектировании двигателя.

9.3 Простые машины | Техасский шлюз

Цели обученияПростые машиныРасчет механических преимуществ и эффективности простых машинЗадания на практикуПроверьте свое понимание

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать простые и сложные механизмы
• Расчет механического преимущества и эффективности простых и сложных машин

«>

Ключевые термины раздела

сложная машина	выход эффективности	идеальное механическое преимущество
наклонная плоскость	входная работа	рычаг
механическое преимущество	выходная работа	шкив
винт	простая машина	клин
колесо и ось

Простые машины

Простые машины облегчают работу, но не уменьшают ее объем. Почему простые машины не могут изменить объем выполняемой вами работы? Напомним, что в закрытых системах общее количество энергии сохраняется. Машина не может увеличить количество энергии, которую вы в нее вкладываете. Итак, чем полезна простая машина? Хотя она не может изменить объем выполняемой вами работы, простая машина может изменить величину силы, которую вы должны приложить к объекту, и расстояние, на котором вы прикладываете силу. В большинстве случаев для уменьшения силы, которую необходимо приложить для выполнения работы, используется простая машина. Обратной стороной является то, что вы должны приложить силу на большее расстояние, потому что произведение силы и расстояния, f d (что равно работе) не меняется.

Давайте посмотрим, как это работает на практике. На рис. 9.8(а) рабочий использует своего рода рычаг, чтобы приложить небольшое усилие на большом расстоянии, в то время как монтировка тянет гвоздь с большой силой на небольшом расстоянии. На рис. 9.8(b) показано, как математически работает рычаг. Сила усилия, приложенная к F _e , поднимает груз (сила сопротивления), который давит вниз в F _р . Треугольный стержень называется точкой опоры; часть рычага между точкой опоры и F _e — плечо усилия, L _e ; а часть слева — это рычаг сопротивления, L _r .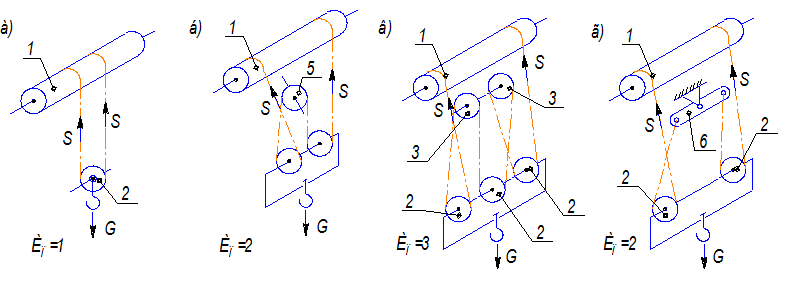 Механическое преимущество — это число, которое говорит нам, во сколько раз простая машина увеличивает силу усилия. Идеальное механическое преимущество, IMA , представляет собой механическое преимущество совершенной машины без потери полезной работы, вызванной трением между движущимися частями. Уравнение для IMA показан на рис. 9.8(b).

Рисунок 9.8 (a) Монтировка представляет собой тип рычага. (b) Идеальное механическое преимущество равно длине плеча усилия, деленному на длину плеча сопротивления рычага.

В общем, IMA = сила сопротивления, F _r , деленная на силу усилия, F _e . IMA также равняется расстоянию, на котором прикладывается усилие, d _e , деленное на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Возвращаясь к сохранению энергии, для любой простой машины работа, вложенная в машину, Вт _i равна работе, производимой машиной, Вт _или . Объединив это с информацией из предыдущих абзацев, мы можем написать

.

Wi=WoFede=FrdrIf  FeFr, затем de>dr.Wi=WoFede=FrdrIf  FeFr, затем de>dr.

Уравнения показывают, как простая машина может производить тот же объем работы, уменьшая величину усилия за счет увеличения расстояния, на котором действует усилие.

Watch Physics

Введение в Mechanical Advantage

В этом видеоролике показано, как рассчитать IMA рычага тремя различными методами: (1) по силе усилия и силе сопротивления; (2) от длин плеч рычагов, и; (3) от расстояния, на котором приложена сила, и расстояния, на которое перемещается груз.

Проверка хватки

Двое детей разного веса катаются на качелях. Как они располагаются относительно точки опоры (точки опоры), чтобы сохранять равновесие?

1. Более тяжелый ребенок сидит ближе к точке опоры.
2. Более тяжелый ребенок сидит дальше от точки опоры.
3. Оба ребенка сидят на равном расстоянии от точки опоры.
4. Так как оба имеют разный вес, они никогда не будут в равновесии.

Некоторые рычаги прикладывают большое усилие к короткому рычагу. Это приводит к тому, что на конце рычага сопротивления действует меньшая сила на большем расстоянии. Примерами этого типа рычага являются бейсбольные биты, молотки и клюшки для гольфа. В другом типе рычага точка опоры находится на конце рычага, а груз — посередине, как в конструкции тачки.

Простая машина, показанная на рис.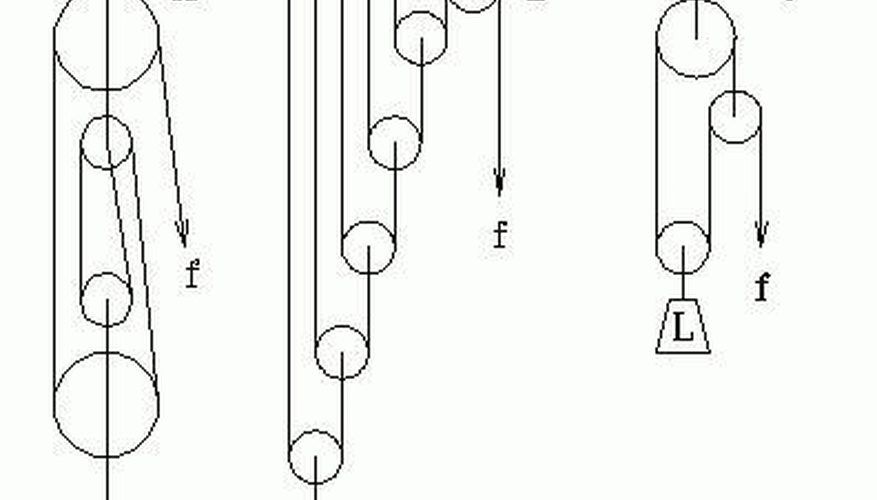 9.9, называется колесом и осью . На самом деле это форма рычага. Разница в том, что рычаг усилия может вращаться по полному кругу вокруг точки опоры, которая является центром оси. Сила, приложенная к внешней стороне колеса, вызывает большее усилие, приложенное к веревке, обернутой вокруг оси. Как показано на рисунке, идеальное механическое преимущество рассчитывается путем деления радиуса колеса на радиус оси. Любое устройство с кривошипным приводом является примером колеса и оси.

Рисунок 9.9 Сила, приложенная к колесу, действует на его ось.

Наклонная плоскость и клин — две формы одной и той же простой машины. Клин — это просто две наклонные плоскости, расположенные спиной к спине. На рис. 9.10 показаны простые формулы для расчета IMA s этих машин. Все наклонные мощеные поверхности для ходьбы или вождения представляют собой наклонные плоскости. Ножи и головки топоров являются примерами клиньев.

Рис.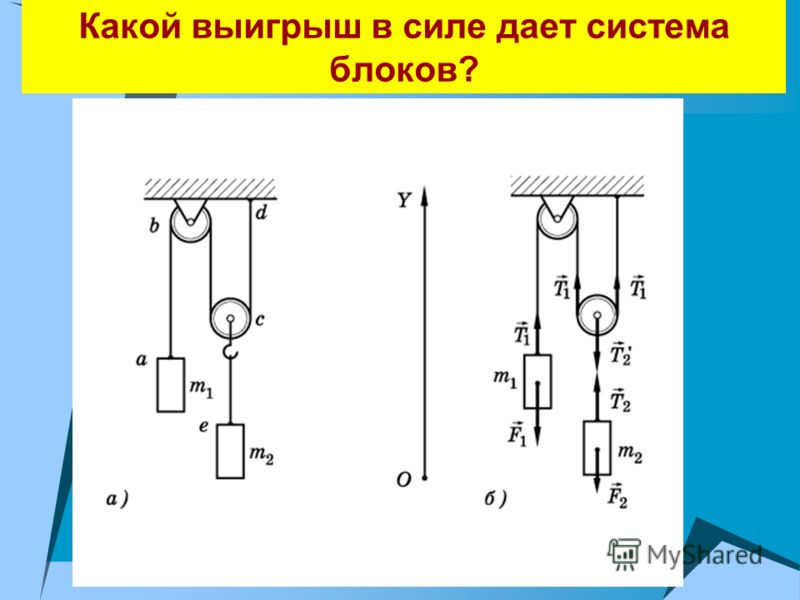 9.10 Слева показана наклонная плоскость, справа — клин.

Винт, показанный на рис. 9.11, на самом деле представляет собой рычаг, прикрепленный к круглой наклонной плоскости. Шурупы по дереву (конечно) также являются примерами шурупов. Рычажная часть этих винтов представляет собой отвертку. В формуле для IMA расстояние между резьбами винтов называется шагом и имеет символ P .

Рисунок 9.11 Показанный здесь винт используется для подъема очень тяжелых предметов, например, угла автомобиля или дома на небольшое расстояние.

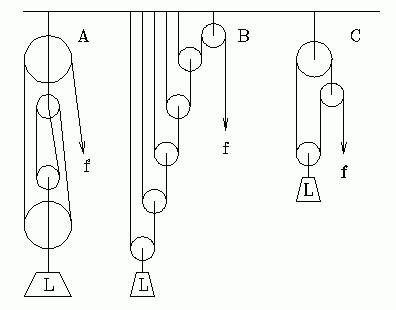
На рис. 9.12 показаны три различные системы шкивов. Из всех простых машин механическое преимущество легче всего рассчитать для шкивов. Просто посчитайте количество канатов, поддерживающих груз. Это IMA . И снова мы должны применять силу на более длинном расстоянии, чтобы умножить силу. Чтобы поднять груз на 1 метр с помощью шкивной системы, нужно потянуть за Н метра веревки. Системы шкивов часто используются для подъема флагов и оконных жалюзи и являются частью механизма строительных кранов.

Рисунок 9.12 Здесь показаны три системы шкивов.

Watch Physics

Механические преимущества наклонных плоскостей и шкивов

В первой части этого видео показано, как рассчитать IMA систем шкивов. В последней части показано, как рассчитать IMA наклонной плоскости.

Нажмите, чтобы просмотреть содержание

Проверка захвата

Как можно использовать систему шкивов, чтобы поднять легкий груз на большую высоту?

1. Уменьшить радиус шкива.
2. Увеличить количество шкивов.
3. Уменьшите количество канатов, поддерживающих груз.
4. Увеличьте количество канатов, поддерживающих груз.

Сложная машина представляет собой комбинацию двух или более простых машин.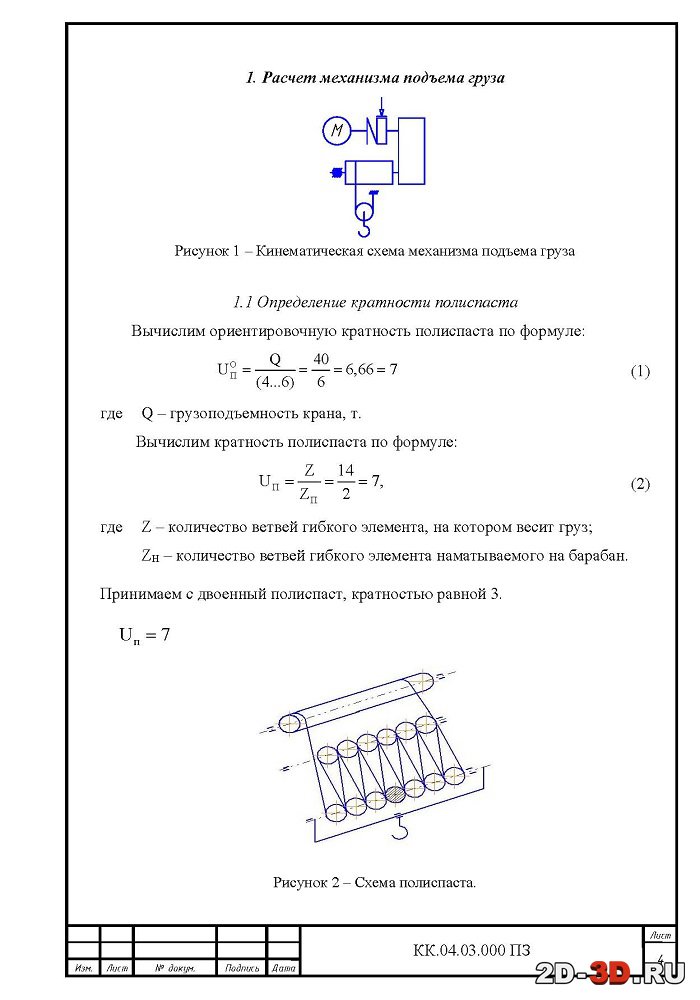 Кусачки на рис. 9.13 сочетают в себе два рычага и два клина. Велосипеды включают в себя колеса и оси, рычаги, винты и шкивы. Автомобили и другие транспортные средства представляют собой комбинации многих машин.

Рис. 9.13 Кусачки для проволоки — обычное сложное оборудование.

Расчет механических преимуществ и эффективности простых машин

В общем, IMA = сила сопротивления, F _r , деленная на силу усилия, F _e . IMA также равно расстоянию, на которое прикладывается усилие, d _e , деленному на расстояние, которое проходит груз, d _r .

IMA=FrFe=dedrIMA=FrFe=dedr

Вернитесь к обсуждениям каждой простой машины для конкретных уравнений для IMA для каждого типа машины.

Никакие простые или сложные машины не обладают фактическими механическими преимуществами, рассчитанными по уравнениям IMA . В реальной жизни часть прикладной работы всегда заканчивается напрасной тратой тепла из-за трения между движущимися частями. И входная работа ( W _i ), и выходная работа ( W _o ) являются результатом действия силы, F , действующей на расстоянии, d .

Wi=Fidi     Wo=FodoWi=Fidi  and  Wo=Fodo

Выходная эффективность машины — это просто работа на выходе, деленная на работу на входе, и обычно умножается на 100, так что это выражается в процентах.

% эффективности=WoWi×100% эффективности=WoWi×100

Посмотрите на изображения простых машин и подумайте, какая из них будет иметь наибольшую эффективность. Эффективность связана с трением, а трение зависит от гладкости поверхностей и от площади соприкасающихся поверхностей. Как смазка повлияет на эффективность простой машины?

Рабочий пример

Эффективность рычага

Входная сила в 11 Н, действующая на плечо рычага, перемещается на 0,4 м, что поднимает груз массой 40 Н, опирающийся на плечо сопротивления, на расстояние 0,1 м. Каков КПД машины?

Стратегия

Составьте уравнение для эффективности простой машины, % эффективности = WoWi × 100, % эффективности = WoWi × 100, и рассчитайте Вт _o и Вт _i . _{Оба значения работы являются продуктом Fd .}

Решение

Wi=FidiWi=Fidi = (11)(0,4) = 4,4 Дж и Wo=FodoWo=Fodo = (40)(0,1) = 4,0 Дж, тогда % эффективности=WoWi×100=4,04,4×100 =91% % эффективность=WoWi×100=4,04.4×100=91% 

Обсуждение

КПД реальных машин всегда будет меньше 100 процентов из-за работы, которая преобразуется в недоступное тепло за счет трения и сопротивления воздуха. W _o и W _i всегда можно рассчитать как силу, умноженную на расстояние, хотя эти величины не всегда так очевидны, как в случае с рычагом.

Практические задачи

Какова IMA наклонной плоскости длиной 5 м и высотой 2 м?

1. 0,4
2. 2,5
3. 0,4 м
4. 2,5 м

Если система шкивов может поднять груз 200 Н с усилием 52 Н и имеет КПД почти 100 %, сколько канатов поддерживает груз?

1. Требуется 1 веревка, так как фактическое механическое преимущество составляет 0,26.
2. Требуется 1 веревка, потому что фактическое механическое преимущество равно 3,80.
3. Требуется 4 веревки, поскольку фактическое механическое преимущество составляет 0,26.
4. Требуется 4 веревки, потому что фактическое механическое преимущество составляет 3,80.