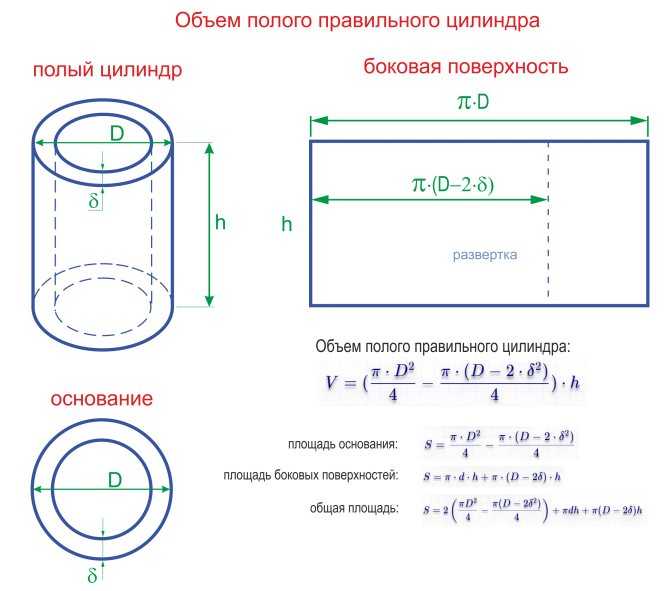
Вагоностроение — цистерны | АО Алтайвагон
| Технические характеристики | |
|---|---|
| объем котла, м3 | 72,4 |
| грузоподъемность, т | 67,0 |
| масса тары минимальная, т | 26,0 |
| масса тары максимальная, т | 27,0 |
| ширина колеи, мм | 1520 |
| количество осей, шт. | 4 |
| максимальная расчетная статистическая нагрузка от колесной пары на рельсы, кН(тс) | 230,5 (23,5) |
| база вагона, мм | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 3 165 |
| высота вагона максимальная, мм | 4 650 |
| диаметр котла внутренний, мм | 3 000 |
| длина котла наружная, номинальная, мм | 10 774 |
| длина котла наружная, по пароподогревательной рубашке, мм | 10 880 |
| рабочее давление в котле(давление паров), МПа (кгс/см2) | 0,070 (0,7) |
| расчетное давление в котле, МПа (кгс/см2) | 0,325 (3,25) |
| габарит по ГОСТ 9238 | 0-ВМ |
| конструкционная скорость, км/ч | 120 |
| модель тележки тип 2, ГОСТ 9246 | 18-2129 |
| Технические характеристики | |
|---|---|
| объем котла, м3 | 83,9 |
| грузоподъемность, т | 52,0 |
| масса тары минимальная, т | 35,8 |
| масса тары максимальная, т | 37,5 |
количество осей, шт. | 4 |
| максимальная расчетная статистическая нагрузка от колесной пары на рельсы, кН(тс) | 220,5 (22,5) |
| база вагона, мм3 | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 3 260 |
| высота вагона максимальная, мм | 5 250 |
| диаметр котла внутренний, мм | 3 200 |
| длина котла наружная, мм | 11 000 |
| рабочее давление в котле, МПа (кгс/см2) | 2,00 (20,0) |
| расчетное давление в котле, МПа (кгс/см2) | 2,11 (21,1) |
| габарит по ГОСТ 9238-2013 | 1-Т |
| конструкционная скорость, км/ч | 120 |
| модель тележки (тип 2 по ГОСТ 9246-2013) | 18-2128 |
| Технические характеристики | |
|---|---|
| объем котла, м3 | 85,5 |
| грузоподъемность, т | 66,0 |
| масса тары минимальная, т | 27,0 |
| масса тары максимальная, т | 28,0 |
количество осей, шт. | 4 |
| максимальная статическая расчетная нагрузка от колесной пары на рельсы, кН(тс) | 230,5 (23,5) |
| база вагона, мм | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 3 345 |
| высота вагона максимальная, мм | 4 830 |
| диаметр котла внутренний, мм | 3 200 |
| длина котла наружная, мм | 10 800 |
| расчетное давление в котле, МПа (кгс/см2) | 0,38 (3,8) |
| габарит по ГОСТ 9238-2013 | 1-Т |
| конструкционная скорость, км/ч | 120 |
| модель тележки (тип 2 по ГОСТ 9246-2013) | 18-2128 |
| Технические характеристики | |
|---|---|
| объем котла, м3 | 85,5 |
| грузоподъемность, т | 66,0 |
| масса тары минимальная, т | 27,0 |
| масса тары максимальная, т | 28,0 |
количество осей, шт.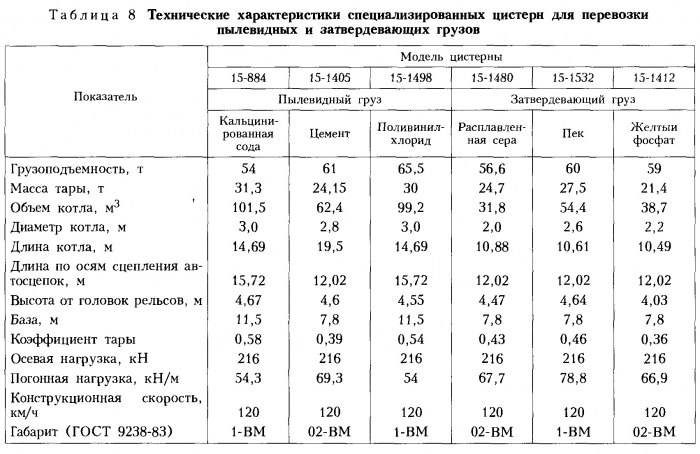 | 4 |
| максимальная статическая расчетная нагрузка от колесной пары на рельсы, кН(тс) | 230,5 (23,5) |
| база вагона, мм | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 3 345,5 |
| высота вагона максимальная, мм | 4 830 |
| диаметр котла внутренний, мм | 3 200 |
| длина котла наружная, мм | 10 800 |
| расчетное давление в котле, МПа (кгс/см2) | 0,38 (3,8) |
| габарит по ГОСТ 9238-2013 | 1-Т |
| конструкционная скорость, км/ч | 120 |
| модель тележки (тип 2 по ГОСТ 9246-2013) | 18-2128 |
| Технические характеристики | |
|---|---|
| объем котла, м3 | 86,5 |
| грузоподъемность (проектная), т, не более | 50,14 |
| масса тары минимальная, т | 36,6 |
| масса тары максимальная, т | 39,0 |
количество осей, шт. | 4 |
| максимальная статическая расчетная нагрузка от колесной пары на рельсы, кН(тс) | 218,63 (22,29) |
| база вагона, мм | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 3 289 |
| высота вагона максимальная, мм | 5 090 |
| диаметр котла внутренний, мм | 3 220 |
| диаметр котла наружная, мм | 11 200 |
| рабочее давление в котле, МПа (кгс/см2) | 2,14 (21,8) |
| расчетное давление в котле, МПа (кгс/см2) | 2,14 (21,8) |
| давление срабатывания предохранительного клапана, МПа (кгс/см2) | 2,2 (22,4) |
| габарит по ГОСТ 9238-2013 | 1-Т |
| конструкционная скорость, км/ч | 120 |
| модель тележки (тип 2 ГОСТ 9246-2013) | 18-2128 |
| Технические характеристики | |
|---|---|
| объем котла полный, м3 | 72,2 |
| объем котла полезный, м3 | 61,0 |
| грузоподъемность, т | 61 |
| масса тары минимальная, т | 31,0 |
| масса тары максимальная, т | 33,0 |
количество осей, шт. | 4 |
| база вагона, мм | 7 800 |
| длина по осям сцепления автосцепок, мм | 12 020 |
| ширина вагона максимальная, мм | 12 020 |
| высота вагона максимальная, мм | 5 070 |
| диаметр котла внутренний, мм | 3 000 |
| длина котла наружная с теплоизоляцией, мм | 11 200 |
| расчетное давление в котле, МПа (кгс/см2) | 11 200 |
| давление в змеевике, МПа (кгс/см2), не более | 0,5 (5,0) |
| температура в змеевике, оС, не более | 100 |
| теплоноситель в змеевике | горячая вода |
| габарит по ГОСТ 9238-2013 | 1-Т |
| конструкционная скорость, км/ч | 120 |
| модель тележки (тип 2 по ГОСТ 9246-2013) | 18-2128 |
Масса железнодорожной цистерны. Сколько весит цистерна железнодорожная
Главная > ц >
| Модель | Грузоподъемность, т | Объём кузова, м3 | Масса тары вагона, т |
|---|---|---|---|
| 8-осная цистерна для нефтепродуктов, модель 15-871 | 120 | 140 | 48,8 |
| 8-осная цистерна для нефти, модель 15-880 | 125 | 159 | 51 |
| 4-осная цистерна для бензина и светлых нефтепродуктов, модель 15-869 | 62 | 88,6 | 23,5 |
| 4-осная цистерна для вязких нефтепродуктов, модель 15-1566 | 63,5 | 73,17 | 24,23 |
| 4-осная цистерна для цемента, модель 15-1405 | 61 | 62,36 | 24,15 |
| 4-осная цистерна для серной кислоты, модель 15-1401 | 60 | 32,68 | 21,6 |
| 4-осная цистерна для слабой азотной кислоты, модель 15-1404 | 61,5 | 46,86 | 22,33 |
| 4-осная цистерна для соляной кислоты, модель 15-1554 | 62 | 54,06 | 22,5 |
| 4-осная цистерна для пропана, модель 15-1407 | 22,9 | 54 | 35,2 |
| 8-осная цистерна для аммиака, модель 15-1581 | 92,3 | 161,5 | 77 |
| 4-осная цистерна для аммиака, модель 15-1597 | 43 | 75,5 | 38,4 |
| 4-осная цистерна для хлора, модель 15-1556 | 57,5 | 46 | 29,4 |
| 4-осная цистерна для молока, модель 15-886 | 31,2 | 30,24 | 23,3 |
| 4-осная цистерна для спирта, модель 15-1454 | 59 | 73,1 | 23,2 |
| 4-осная цистерна для виноматериалов, модель 15-1593 | 63 | 60,67 | 25 |
| 8-осная цистерна для порошкообразных грузов, модель 15-1445 | 119 | 130 | 52,7 |
| 4-осная цистерна для сжиженных углеводородных газов, модель 15-1200 | 31 | 50 | 36 |
Случайные записи — cколько весит:
трава свежескошенная, 1 м3
статуя Свободы (США)
грибы сушеные, 1 литр
объектив Canon EF 50mm f/1.
утюг Braun FreeStyle 530/SI6591
утюг Panasonic NI-E200
метеорит, самый большой
Объем кубического или прямоугольного резервуара – Math for Trades: Volume 2
Volume
Нажмите кнопку воспроизведения в следующем аудиоплеере, чтобы слушать, пока вы читаете этот раздел
Если бы вас попросили описать объем предмета, как бы это выглядело? Как бы вы описали единицы, в которых будут производиться ваши расчеты?
В этой главе рассматривается расчет объема и единицы измерения, используемые при расчете объема.
В предыдущей главе мы имели дело с периметром, который представляет собой линейное измерение. Как мы выяснили, периметр является одномерным и по существу приобретает характеристики линии. Хорошим примером периметра может быть прогулка по футбольному полю. Вы бы прошлись по периметру поля.
Затем мы взглянули на площадь, которая представляет собой двумерное измерение.
Хорошим примером этого является столешница. Если бы вы взяли кисть и перекрасили верхнюю часть стола, вы бы закрасили область столешницы.
Имея дело с объемом, мы добавляем еще одно измерение, и в результате объем становится трехмерным измерением. Хорошим примером трехмерного объекта может быть планета Земля.
Вот еще одно визуальное представление каждого из трех. Каждая линия представляет собой плоскость.
Теперь вернемся к юнитам. Когда мы имеем дело с линейными измерениями, мы имеем дело с единицами измерения такими, какие они есть. Под этим я подразумеваю, что мы получим ответ в метрах, футах, дюймах, сантиметрах и так далее.
Когда мы имеем дело с площадью, мы продолжаем иметь дело с такими единицами, как метры, но они возведены в квадрат, чтобы показать, что они имеют два измерения. Например, площадь квартиры может составлять 1200 квадратных футов или 1200 футов². Квадратность ножек указывает на два измерения, такие как ширина И длина. 9{3}[/латекс]
«3» в данном случае представляет три измерения и отвечает за термин «кубический», когда мы произносим его.
Теперь мы готовы идти дальше и узнать формулу объема конкретных предметов.
Когда произносится слово «куб», мы можем думать о квадрате, но только с дополнительным измерением. Каждое измерение квадрата идентично, и куб следует той же логике.
Если вы добавите третье измерение, вы получите все возможные измерения одинаковыми. Взгляните на один из самых известных кубов в мире:
Чтобы найти объем куба, нам нужно перемножить три стороны. Более конкретно, мы рассмотрим умножение длины, ширины и высоты. Поскольку все три стороны одинаковы, формула выглядит следующим образом:
[латекс]\Большой \текст{объем куба} = \текст{сторона} \times \текст{сторона} \times \text{сторона}[/латекс]
Найти площадь куба довольно просто. Все, что вам нужно знать, это длину одной стороны, и у вас есть вся необходимая информация.
Найдите объем куба, если одна сторона равна 7 дм.
Шаг 1: Запишите формулу.
[латекс]\Большой \текст{объем куба} = \текст{сторона} \times \текст{сторона} \times \text{сторона}[/латекс]
Шаг 2: Найдите объем.
{3} \end{array}[/ латекс]
Расчет объема прямоугольного резервуара очень похож на расчет объема куба, за исключением того факта, что все размеры прямоугольного резервуара будут другими. С этого момента мы будем называть его просто танком.
Мы также получаем, что имена переменных в баке разные. Когда мы имели дело с прямоугольником, мы ссылались на переменные длины и ширины.
Теперь мы просто добавляем еще одну переменную, которую назовем «высота».
Опять же, мы работаем с тремя измерениями, и формула будет похожа на формулу куба, только переменная «сторона» будет заменена тремя разными переменными танка.
Формула:
[латекс]\Большой \текст{объем бака} = \текст{длина} \times \text{ширина} \times \text{высота}[/latex]
Рассчитайте объем резервуара, имеющего длину 17 дюймов, ширину 12 дюймов и высоту 13 дюймов.
Шаг 1: 9{3} \end{array}[/latex]
Теперь давайте изменим это и представим ответ в кубических футах.
{3} \end{массив}[/латекс] 9{3}= 1,53 \end{array}[/latex]
Давайте рассмотрим еще один пример и еще раз изменим вопрос.
Найдите ширину резервуара, имеющего длину 22 дюйма, высоту 14 дюймов и общий объем 3080 кубических дюймов.
Шаг 1: Запишите формулу.
[латекс]\Большой \текст{объем} = \текст{длина} \times \text{ширина} \times \text{высота}[/latex]
Шаг 2: Переставьте формулу для определения ширины . 9{3}}{22 \text{ дюймов} \times 14 \text{ дюймов}} \\ \text{ширина} = 10 \text{ дюймов} \end{массив}[/latex]
Попробуйте сами ответить на пару практических вопросов. Не забудьте проверить видео ответы, чтобы увидеть, как вы это сделали.
Лайл работает в газовой компании под названием «Ночное и дневное отопление». Он проектирует систему отопления для здания, спроектированного эксцентричным архитектором. Здание имеет форму куба, одна из сторон которого составляет 30 футов.
Перед проектированием системы Лайл должен учитывать объем здания.
Каков объем здания в кубе?
Кейт владеет компанией по установке септических резервуаров в сельской местности Британской Колумбии, и она только что наняла Рэйчел, которая родом из Восточной Африки и никогда раньше не устанавливала септические системы.
Резервуар предназначен для дома с четырьмя спальнями и должен иметь общий объем не менее 170 кубических футов, по словам инженера, разработавшего систему. Размеры резервуара, который они планируют установить, указаны ниже. Учитывая эти размеры, будет ли септик достаточно большим, чтобы удовлетворить требования инженера.
Длина = 7,5 футов
Ширина = 5,25 футов
Высота = 4,5 фута
Что такое объем куба? Значение, формула, вывод, примеры
Что такое объем куба?
Куб – это трехмерное твердое тело с шестью квадратными гранями одинаковой длины. Вся площадь, занимаемая кубом, называется его объемом. Если у нас есть куб, и мы наполняем его водой, то количество воды, которое помещается внутри куба, называется его объемом.
Родственные игры
Примеры объема куба из повседневной жизни
- Если мы наполним картонную коробку шариками конфетти, количество шариков конфетти, которые поместятся в картонную коробку, покажет ее объем.
- Если мы наполним кубический аквариум водой, то количество воды, залитой внутрь, будет его объемом.
Связанные рабочие листы
Каков объем куба?
Точно так же, как площадь представляет собой количество пространства, занимаемого двухмерным объектом, объем определяется как пространство, занимаемое трехмерным объектом.
Рассмотрим квадратный лист бумаги со стороной s. Его площадь будет s²; теперь, если мы сложим их друг над другом до высоты s, то объем куба можно будет найти, умножив площадь основания (s²) на высоту (s).
Таким образом, объем куба = s² ✕ s = s³
Объем куба также можно найти по количеству кубических единиц, необходимых для полного заполнения куба.
Все стороны единичного куба имеют длину 1 единицу.
Итак, объем единичного куба = 1 единица ✕ 1 единица ✕ 1 единица = 1 кубическая единица.
Теперь найдем объем куба со стороной = 4 единицы.
Объем куба будет равен количеству единичных кубов, составляющих куб.
В каждом ряду по 16 кубиков.
Куб со стороной 4 единицы состоит из 64 единичных кубов. Следовательно, его объем составляет 64 кубических единицы.
Объем куба ФормулаЧтобы найти объем куба, нам нужно знать длину любого ребра куба. Длину нужно умножить на себя трижды, чтобы получить объем.
Объем измеряется в кубических единицах. Например, кубические метры (м 3 ), кубические сантиметры (см 3 ) и т. д.
Например, если известно, что длина ребра равна 6 см, то объем куба будет равен 6 × 6 × 6 = 216, а единицей измерения будет см 3 ; здесь объем куба равен 216 см 3 .
Где мы используем объем куба в повседневной жизни?
Мы можем видеть много примеров объема куба в повседневной жизни.
- Резервуар для воды в форме куба может хранить воду, равную объему куба.
- Объем воздуха, занимаемый кубической комнатой.
- Объем древесины, необходимый для постройки твердого кубического блока.
- Перед упаковкой конфет в коробки необходимо измерить объем кубических конфет, чтобы точно знать, сколько места они займут.
Заключение
Объем куба является мерой пространства, занимаемого воздухом внутри него. Используется во многих сферах повседневной жизни. Комната здания или дома может иметь форму куба. Пространство внутри него, где мы живем и работаем, является его объемом. Если вас интересуют более простые и краткие ресурсы по кубам или другим математическим темам, например, что такое куб?, что такое единичный куб? и т. д., вы можете загрузить приложение Splashlearn.
Чтобы получить дополнительные материалы по математике для учителей, бесплатно зарегистрируйтесь на Splashlearn.com.
Решенные примеры
- Каков объем куба, если его ребро равно 2 см?
Решение:
Учитывая, что S = 2 см
объем куба = S × S × S
SO SO, SO, SO, VOMES 2 × S
SO, SO, SO, DADE DAD -DADS 2 × S
SO, SO, DADE DADES 2 × S
SO, SO × S
SO, SO × S
.
2 = 8 см 3
Таким образом, общий объем куба с ребром 2 см равен 8 см 3 .
- Объем куб.контейнера 343 м 3 . Найдите длину стороны контейнера.
Solution:
Volume of a cube = s × s × s
343 = s × s × s
$\sqrt[3]{ 343}$ = s
$\sqrt[3]{7 × 7 × 7}$ = s
Итак, длина стороны контейнера равна 7 м.
- Найдите объем кубика сахара со стороной 5 см.
Решение:
Учитывая, что с = 5 см
Объем куба = с × с × с
х 5 х 5 объем данного куба, см 3 . Таким образом, общий объем куба с ребром 5 см равен 125 см 3 .Практические задачи
1
Каков объем куба, длина ребра которого равна 10 см? 9{3}}{9}$
Связан ли объем куба с объемом конуса?
Нет, объем конуса не связан с объемом куба.
